题目内容
已知正方形ABCD，E、F分别是CD、AD的中点，BE、CF交于点P．求证BE⊥CF．
考点：空间中直线与直线之间的位置关系
专题：空间位置关系与距离
分析：充分利用正方形发性质可以判断△BCE≌△CDF，利用三角形全等的性质可得∠BEC=∠CFD，利用三角形的内角和定理可证．
解答：
证明：因为已知ABCD是正正方形，
所以BC=CD，∠BCE=∠CDF=90°
E、F分别是CD、AD的中点，
所以CE=DF，
所以△BCE≌△CDF，
所以∠BEC=∠CFD，
又∠CFD+∠DCF=90°，
所以∠BEC+∠DCF=90°，
在△PCE中，∠CPE=180°-∠BEC-∠DCF=90°，
所以BE⊥CF．
所以BC=CD，∠BCE=∠CDF=90°
E、F分别是CD、AD的中点，
所以CE=DF，
所以△BCE≌△CDF，
所以∠BEC=∠CFD，
又∠CFD+∠DCF=90°，
所以∠BEC+∠DCF=90°，
在△PCE中，∠CPE=180°-∠BEC-∠DCF=90°，
所以BE⊥CF．
点评：本题考查了正方形的性质以及三角形全等的判定定理和性质定理的运用，属于基础题．
练习册系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
已知点A，B的极坐标分别为（3，
）和（-3，
），则A和B之间的距离等于（ ）
| π |
| 4 |
| π |
| 12 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
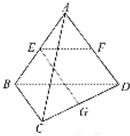如图所示，已知空间四边形ABCD的每条边和对角线长都等于1，点E、F分别是AB、AD的中点，则