题目内容
已知集合T={4,4t,4t2},M={4,4-d,4-2d},其中d,t∈R,若M=T,求t和d的值.
考点:集合的相等
专题:计算题,集合
分析:集合相等,则元素相同,注意集合内元素满足无序性与互异性.
解答:
解:∵集合元素的互异性,
∴4t≠4t2,且4-d≠4-2d,
解得:t≠0,且t≠1,d≠0,
当4t=4-d时,4t2=4-2d,解得:t=1,d=0 (舍去);
当4t=4-2d时,4t2=4-d,解得:t=1(舍去),或t=-1/2,
∴t=-1/2,此时d=3,
∴t=-1/2,d=3.
∴4t≠4t2,且4-d≠4-2d,
解得:t≠0,且t≠1,d≠0,
当4t=4-d时,4t2=4-2d,解得:t=1,d=0 (舍去);
当4t=4-2d时,4t2=4-d,解得:t=1(舍去),或t=-1/2,
∴t=-1/2,此时d=3,
∴t=-1/2,d=3.
点评:本题考查了集合相等的判断及集合内元素的特征,属于基础题.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
已知A、B、C为△ABC的三个内角,且关于x的方程(1+x2)sinA+2xsinB+(1-x2)sinC=0有两个相等实根,则△ABC的形状为( )
| A、锐角三角形 |
| B、直角三角形 |
| C、钝角三角形 |
| D、等边三角形 |
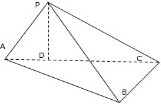 如图,在三棱锥P-ABC中,PD⊥面ABC于点D,且点D在AC上,PA=PB=PC=3,设AB=BC=
如图,在三棱锥P-ABC中,PD⊥面ABC于点D,且点D在AC上,PA=PB=PC=3,设AB=BC=