题目内容
已知数列{an}是公差大于零的等差数列,数列{bn}为等比数列,且a1=1,b1=2,b2-a2=1,a3+b3=13
(Ⅰ)求数列{an}和{bn}的通项公式
(Ⅱ)设cn=anbn,求数列{cn}前n项和Tn.
(Ⅰ)求数列{an}和{bn}的通项公式
(Ⅱ)设cn=anbn,求数列{cn}前n项和Tn.
考点:数列的求和,等差数列的性质
专题:等差数列与等比数列
分析:(Ⅰ)设数列{an}的公差为d(d>0),数列{bn}的公比为q,由题意列方程组求得公差和公比,代入等差数列和等比数列的通项公式得答案;
(Ⅱ)把数列{an}和{bn}的通项公式代入cn=anbn,然后直接利用错位相减法求数列{cn}前n项和Tn.
(Ⅱ)把数列{an}和{bn}的通项公式代入cn=anbn,然后直接利用错位相减法求数列{cn}前n项和Tn.
解答:
解:(Ⅰ)设数列{an}的公差为d(d>0),数列{bn}的公比为q,
由已知得:
,解得:
,
,
∵d>0,∴d=2,q=2,
∴an=1+2(n-1)=2n-1,bn=2×2n-1=2n,
即an=2n-1(n∈N*),bn=2n(n∈N*);
(Ⅱ)∵cn=anbn=(2n-1)2n,
∴Tn=1×2+3×22+5×23+…+(2n-1)×2n ①,
2Tn=1×22+3×23+5×24+…+(2n-1)×2n+1 ②,
②-①得:Tn=-1×2-2×22-2×23-…-2×2n+(2n-1)×2n+1
=-2-23-24-…-2n+1+(2n-1)×2n+1
=-2-
+(2n-1)×2n+1
=6+(2n-3)×2n+1.
由已知得:
|
|
|
∵d>0,∴d=2,q=2,
∴an=1+2(n-1)=2n-1,bn=2×2n-1=2n,
即an=2n-1(n∈N*),bn=2n(n∈N*);
(Ⅱ)∵cn=anbn=(2n-1)2n,
∴Tn=1×2+3×22+5×23+…+(2n-1)×2n ①,
2Tn=1×22+3×23+5×24+…+(2n-1)×2n+1 ②,
②-①得:Tn=-1×2-2×22-2×23-…-2×2n+(2n-1)×2n+1
=-2-23-24-…-2n+1+(2n-1)×2n+1
=-2-
| 23(1-2n-1) |
| 1-2 |
=6+(2n-3)×2n+1.
点评:本题考查了等差数列和等比数列的通项公式,考查了错位相减法求数列的和,是中档题.

练习册系列答案
相关题目
函数f(x)=
x+log2x的零点所在区间为( )
| π |
| 2 |
A、[0,
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
设a∈R,若函数f(x)=ex-ax,x∈R有大于零的极值点,则( )
| A、a<1 | ||
| B、a>1 | ||
C、a<
| ||
D、a>
|
对任意的[-
,
]时,不等式x2+2x-a≤0恒成立,则实数a的取值范围是( )
| 1 |
| 2 |
| 1 |
| 2 |
| A、(-∞,0] | ||
| B、(-∞,3] | ||
| C、[0,+∞) | ||
D、[
|
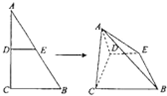 直角三角形ABC中,∠ACB=90°,AB=2BC=2,D、E分别为AC、AB边的中点.将△ADE沿DF折起,使△ADE沿DE折起,使△ADC为等边三角形,如图所示.
直角三角形ABC中,∠ACB=90°,AB=2BC=2,D、E分别为AC、AB边的中点.将△ADE沿DF折起,使△ADE沿DE折起,使△ADC为等边三角形,如图所示.