题目内容
2.已知直线x-y+2=0与圆C:(x-3)2+(y-3)2=4交于点A,B,过弦AB的中点的直径为MN,则四边形AMBN的面积为( )| A. | $8\sqrt{2}$ | B. | 8 | C. | $4\sqrt{2}$ | D. | 4 |
分析 求出圆心到直线的距离,可得|AB|,即可求出四边形AMBN的面积.
解答 解:圆C:(x-3)2+(y-3)2=4的圆心C(3,3),半径为2,则
圆心到直线的距离为d=$\frac{|3-3+2|}{\sqrt{2}}$=$\sqrt{2}$,
∴|AB|=2$\sqrt{4-2}$=2$\sqrt{2}$,
∴四边形AMBN的面积为2$\sqrt{2}•4•\frac{1}{2}$=4$\sqrt{2}$,
故选C.
点评 本题考查直线与圆的位置关系,考查四边形AMBN的面积,属于中档题.

练习册系列答案
相关题目
13.函数y=f(x)在x=x0处的导数f′(x0)的几何意义是( )
| A. | 在点x0处的斜率 | |
| B. | 在点(x0,f(x0))处的切线与x轴所夹的锐角的正切值 | |
| C. | 曲线y=f(x)在点(x0,f(x0))处切线的斜率 | |
| D. | 点(x0,f(x0))与点(0,0)连线的斜率 |
10.已知集合U=R,A={x|(x-2)(x+1)≤0},B={x|0≤x<3},则∁U(A∪B)=( )
| A. | (-1,3) | B. | (-∞,-1]∪[3,+∞) | C. | [-1,3] | D. | (-∞,-1)∪[3,+∞) |
17.已知△ABC中,满足b=2,B=60°的三角形有两解,则边长a的取值范围是( )
| A. | $\frac{\sqrt{3}}{2}$<a<2 | B. | $\frac{1}{2}$<a<2 | C. | 2<a<$\frac{4\sqrt{3}}{3}$ | D. | 2<a<2$\sqrt{3}$ |
11.欧拉(LeonhardEuler,国籍瑞士)是科学史上最多产的一位杰出的数学家,他发明的公式eix=cosx+isinx(i为虚数单位),将指数函数的定义域扩大到复数,建立了三角函数和指数函数的关系,这个公式在复变函数理论中占有非常重要的地位,被誉为“数学中的天桥”.根据此公式可知,表示的复数${e^{\frac{2π}{3}i}}$在复平面内位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
16.{an}是a1=2,d=2的等差数列,其前n项和公式为( )
| A. | Sn=n2-n | B. | Sn=n2-2n | C. | Sn=n2+n | D. | Sn=n2+2n |
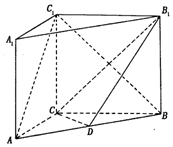 如图,在直三棱柱ABC-A1B1C1中,点D是AB的中点,$A{A_1}=AC=CB=\frac{{\sqrt{2}}}{2}AB$
如图,在直三棱柱ABC-A1B1C1中,点D是AB的中点,$A{A_1}=AC=CB=\frac{{\sqrt{2}}}{2}AB$