题目内容
12.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$,其中|$\overrightarrow{a}$|=$\sqrt{3}$,|$\overrightarrow{b}$|=2,且($\overrightarrow{a}$-$\overrightarrow{b}$)⊥$\overrightarrow{a}$,则向量$\overrightarrow{a}$和$\overrightarrow{b}$的夹角是$\frac{π}{6}$.分析 利用向量垂直的数量积为0列出方程;利用向量的平方等于向量模的平方及向量的数量积公式将方程用模与夹角表示求出夹角.
解答 解:设两个向量的夹角为θ,
∵|$\overrightarrow{a}$|=$\sqrt{3}$,|$\overrightarrow{b}$|=2,且($\overrightarrow{a}$-$\overrightarrow{b}$)⊥$\overrightarrow{a}$,
∴($\overrightarrow{a}$-$\overrightarrow{b}$)•$\overrightarrow{a}$=|$\overrightarrow{a}$|2-$\overrightarrow{a}$•$\overrightarrow{b}$=|$\overrightarrow{a}$|2-|$\overrightarrow{a}$|•|$\overrightarrow{b}$|cosθ=3-2$\sqrt{3}$cosθ=0,
解得cosθ=$\frac{\sqrt{3}}{2}$,
∵0≤θ≤π,
∴θ=$\frac{π}{6}$,
故答案为:$\frac{π}{6}$.
点评 本题考查向量垂直的充要条件、考查向量模的平方等于向量的平方、考查向量的数量积公式.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案
相关题目
3.执行如图所示的程序框图,若输出的S=18,则判断框内应填入的条件是( )


| A. | k>2? | B. | k>3? | C. | k>4? | D. | k>5? |
20.函数f(x)=$\left\{\begin{array}{l}{ax+b,x<-1}\\{ln(x+a),x≥-1}\\{\;}\end{array}\right.$的图象如图所示,则f(-3)等于( )


| A. | -$\frac{1}{2}$ | B. | -$\frac{5}{4}$ | C. | -1 | D. | -2 |
17.某校高一、高二、高三年级学生人数分别是400,320,280.采用分层抽样的方法抽取50人,参加学校举行的社会主义核心价值观知识竞赛,则样本中高三年级的人数是( )
| A. | 20 | B. | 16 | C. | 15 | D. | 14 |
1.若函数y=2x上存在点(x,y)满足约束条件$\left\{\begin{array}{l}x+y-3≤0\\ x-2y-3≤0\\ x≥m\end{array}\right.$,则实数m的最大值为( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{{\sqrt{2}}}{2}$ | D. | 2 |
2.某单位对360位应聘者进行了2个科目的测试,每个科目的成绩由高到低依次为优秀、良好和一般,从所有应聘者的成绩中随机抽取27个数据统计如下:
由表可见,科目一成绩为优秀且科目二成绩为良好的有2人,若将表中数据的频率设为概率,则估计有80位应聘者科目一的乘积高于科目二的成绩.
(Ⅰ)估计两科成绩相同的应聘者的人数;
(Ⅱ)从所有科目一成绩为良好的应聘者中随机抽取3人,设这3人成绩中优秀科目总数为ξ,求随机变量ξ的分布列及其数学期望Eξ;
(Ⅲ)根据两科测试成绩,每位应聘者可能属于9个不同的成绩组之一,设表中两科成绩不同的各组人数的方差为s12,科目一成绩不高于科目二成绩的各组人数的方差为s22,比较s12与s22的大小.(只写结论即可)
 | 优秀 | 良好 | 一般 |
| 优秀 | b | 2 | 3 |
| 良好 | 3 | 4 | a |
| 一般 | 3 | 3 | 3 |
(Ⅰ)估计两科成绩相同的应聘者的人数;
(Ⅱ)从所有科目一成绩为良好的应聘者中随机抽取3人,设这3人成绩中优秀科目总数为ξ,求随机变量ξ的分布列及其数学期望Eξ;
(Ⅲ)根据两科测试成绩,每位应聘者可能属于9个不同的成绩组之一,设表中两科成绩不同的各组人数的方差为s12,科目一成绩不高于科目二成绩的各组人数的方差为s22,比较s12与s22的大小.(只写结论即可)
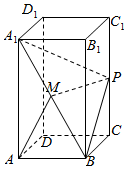 如图,在正四棱柱ABCD-A1B1C1D1中,AD=1,D1D=2,点P为棱CC1的中点.
如图,在正四棱柱ABCD-A1B1C1D1中,AD=1,D1D=2,点P为棱CC1的中点.