题目内容
17.某校高一、高二、高三年级学生人数分别是400,320,280.采用分层抽样的方法抽取50人,参加学校举行的社会主义核心价值观知识竞赛,则样本中高三年级的人数是( )| A. | 20 | B. | 16 | C. | 15 | D. | 14 |
分析 先求出抽取样本的比例是多少,再计算从高三学生中应抽取的人是多少.
解答 解:根据题意,得抽取样本的比例是$\frac{50}{400+320+280}$=$\frac{1}{20}$,
∴从高三学生中应抽取的人数为280×$\frac{1}{20}$=14.
故选:D.
点评 本题考查了分层抽样方法的应用问题,是容易题目.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.等比数列{an}中,a1=1,公比q=2,前n项和为Sn,下列结论正确的是( )
| A. | $?{n_0}∈N*,{a_{n_0}}+{a_{{n_0}+2}}=2{a_{{n_0}+1}}$ | |
| B. | ?n∈N*,an•an+1≤an+2 | |
| C. | ?n∈N*,Sn<an+1 | |
| D. | $?{n_0}∈N*,{a_{n_0}}+{a_{{n_0}+3}}={a_{{n_0}+1}}+{a_{{n_0}+2}}$ |
9.所示的程序框图输出的结果为S=35,则判断框中应填入的关于k的条件是( )


| A. | k>7 | B. | k≤6 | C. | k>6 | D. | k<6 |
6.阅读如图所示的程序框图,运行相应的程序.若输出的S为$\frac{25}{24}$,则判断框中填写的内容可以是( )
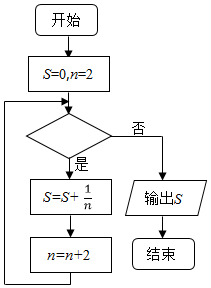

| A. | n=6 | B. | n<6 | C. | n≤6 | D. | n≤8 |
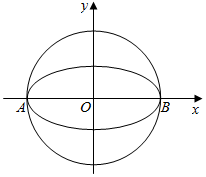 如图,椭圆$W:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{3}}}{2}$,其左顶点A在圆O:x2+y2=16上.
如图,椭圆$W:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{3}}}{2}$,其左顶点A在圆O:x2+y2=16上. 某公司从大学招收毕业生,经过综合测试,录用了14名男生和6名女生,这20名毕业生的测试成绩如茎叶图所示(单位:分).公司规定:
某公司从大学招收毕业生,经过综合测试,录用了14名男生和6名女生,这20名毕业生的测试成绩如茎叶图所示(单位:分).公司规定: