题目内容
投掷四枚不同的金属硬币A、B、C、D,假定A、B两枚正面向上的概率均为
,另两枚C、D为非均匀硬币,正面向上的概率均为a(0<a<1),把这四枚硬币各投掷一次,设?表示正面向上的枚数.
(Ⅰ)若A、B出现一枚正面向上一枚反面向上与C、D出现两枚正面均向上的概率相等,求a的值;
(Ⅱ)求?的分布列及数学期望(用a表示);
(Ⅲ)若出现2枚硬币正面向上的概率都不小于出现1枚和3枚硬币正面向上的概率,求a的取值范围.
| 1 |
| 2 |
(Ⅰ)若A、B出现一枚正面向上一枚反面向上与C、D出现两枚正面均向上的概率相等,求a的值;
(Ⅱ)求?的分布列及数学期望(用a表示);
(Ⅲ)若出现2枚硬币正面向上的概率都不小于出现1枚和3枚硬币正面向上的概率,求a的取值范围.
考点:离散型随机变量的期望与方差,古典概型及其概率计算公式
专题:概率与统计
分析:(Ⅰ)由题意,得2×
×(1-
)=a2,由此能求出a.
(Ⅱ)由题意知?=0,1,2,3,4,分别求出相应的概率,由此能求出?的分布列和?的数学期望.
(Ⅲ)由题意知P(?=2)-P(?=1)≥0.且P(?=2)-P(?=3)≥0,由此能求出a的取值范围.
| 1 |
| 2 |
| 1 |
| 2 |
(Ⅱ)由题意知?=0,1,2,3,4,分别求出相应的概率,由此能求出?的分布列和?的数学期望.
(Ⅲ)由题意知P(?=2)-P(?=1)≥0.且P(?=2)-P(?=3)≥0,由此能求出a的取值范围.
解答:
解:(Ⅰ)由题意,得2×
×(1-
)=a2,
解得a=
…(3分)
(Ⅱ)由题意知?=0,1,2,3,4.…(4分)
P(?=0)=
(1-
)2
(1-a)2=
(1-a)2,…(5分)
P(?=1)=
•
(1-
(1-a)2+
(1-
)2
a(1-a)=
(1-a),…(6分)
P(?=2)=
(
)2
(1-a)2+
(1-
)
a(1-a)+
(1-
)2
a2=
(1+2a-2a2),…(7分)
P(?=3)=
(
a(1-a)+
(1-
)
a2=
,…(8分)
P(?=4)=
(
)2
a2=
a2.…(9分)
∴?的分布列为:
?的数学期望为:E?=1×
(1-a)+2×
(1+2a-2a2)+3×
+4×
a2=2a+1.…(10分)
(Ⅲ)由题意知P(?=2)-P(?=1)=
(1+2a-2a2)-
(1-a)=-
(2a2-4a+1)≥0.
且P(?=2)-P(?=3)=
(1+2a-2a2)-
=-
(2a2-1)≥0.…(12分)
∴
,解得
≤a≤
,
∴a的取值范围是[
,
].…(13分)
| 1 |
| 2 |
| 1 |
| 2 |
解得a=
| ||
| 2 |
(Ⅱ)由题意知?=0,1,2,3,4.…(4分)
P(?=0)=
| C | 0 2 |
| 1 |
| 2 |
| C | 0 2 |
| 1 |
| 4 |
P(?=1)=
| C | 1 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| )C | 0 2 |
| C | 0 2 |
| 1 |
| 2 |
| C | 1 2 |
| 1 |
| 2 |
P(?=2)=
| C | 2 2 |
| 1 |
| 2 |
| C | 0 2 |
| C | 1 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| C | 1 2 |
| C | 0 2 |
| 1 |
| 2 |
| C | 2 2 |
| 1 |
| 4 |
P(?=3)=
| C | 2 2 |
| 1 |
| 2 |
| )2C | 1 2 |
| C | 1 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| C | 2 2 |
| a |
| 2 |
P(?=4)=
| C | 2 2 |
| 1 |
| 2 |
| C | 2 2 |
| 1 |
| 4 |
∴?的分布列为:
| ? | 0 | 1 | 2 | 3 | 4 | ||||||||||
| p |
|
|
|
|
|
| 1 |
| 2 |
| 1 |
| 4 |
| a |
| 2 |
| 1 |
| 4 |
(Ⅲ)由题意知P(?=2)-P(?=1)=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
且P(?=2)-P(?=3)=
| 1 |
| 4 |
| a |
| 2 |
| 1 |
| 4 |
∴
|
2-
| ||
| 2 |
| ||
| 2 |
∴a的取值范围是[
2-
| ||
| 2 |
| ||
| 2 |
点评:本题主要考查n次独立重复试验中恰好发生k次的概率、离散型随机变量的期望与方差、概率的应用等基础知识,考查运算求解能力.属于中档题.

练习册系列答案
相关题目
(
-
)8二项展开式中的常数项为( )
| 3 | x |
| 2 |
| x |
| A、112 | B、-112 |
| C、56 | D、-56 |
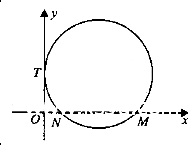 如图,已知圆C与y轴相切于点T(0,2),与x轴正半轴相交于两点M,N(点M必在点N的右侧),且|MN|=3,己知椭圆D:
如图,已知圆C与y轴相切于点T(0,2),与x轴正半轴相交于两点M,N(点M必在点N的右侧),且|MN|=3,己知椭圆D: 如图,△ABC是直角三角形,∠ABC=90°以AB为直径的圆O交AC于点E,点D是BC边的中点,连接OD交圆O于点M.
如图,△ABC是直角三角形,∠ABC=90°以AB为直径的圆O交AC于点E,点D是BC边的中点,连接OD交圆O于点M.