题目内容

化简：
sin(
π
2
+α)cos(
π
2
-α)
cos(π+α)
+
sin(π-α)cos(
π
2
+α)
sin(π+α)
．
考点：运用诱导公式化简求值
专题：三角函数的求值
分析：由条件利用诱导公式进行化简要求的式子，可得结果．
解答： 解：
sin(
π
2
+α)cos(
π
2
-α)
cos(π+α)
+
sin(π-α)cos(
π
2
+α)
sin(π+α)
=
cosα•sinα
-cosα
+
sinα(-sinα)
-sinα
=-sinα+sinα=0．
点评：本题主要考查利用诱导公式进行化简求值，属于基础题．
练习册系列答案
相关题目
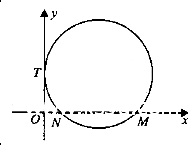如图，已知圆C与y轴相切于点T（0，2），与x轴正半轴相交于两点M，N（点M必在点N的右侧），且|MN|=3，己知椭圆D：
x2
a2
+
y2
b2
=1（a＞b＞0）的焦距等于2|ON|，离心率e=
1
2
；
（1）求圆C和椭圆D的方程；
（2）若过点M斜率不为零的直线l与椭圆D交于A、B两点，求证：直线NA与直线NB的倾角互补．
已知各项均不相等的等差数列{an}的前四项和S4=14，且a1，a3，a7成等比．
（1）求数列{an}的通项公式；
（Ⅱ）设Tn为数列{
1
anan+2
}的前n项和，若Tn≤λ对?n∈N*恒成立，求实数λ的最小值．
已知函数f（x）=
1
2
x3-ax+1．
（Ⅰ）当a=1时，求曲线y=f（x）在点（2，f（2））处的切线方程；
（Ⅱ）在区间[-1，2]内至少存在一个实数x，使得f（x）≤0成立，求实数a的取值范围．
设复数z=a+bi（a，b∈R，a＞0），满足|z|=
10
，且复数（1-2i）z在复平面上对应的点在第二、四象限的角平分线上．
（Ⅰ）求复数z；
（Ⅱ）若
.
z
+
m+i
1-i
（m∈R）为纯虚数，求实数m的值．
方程
3
sinx-cosx=0（x∈[0，2π]）的所有解之和为
 
．
已知直线l的参数方程为
x=
2
2
t
y=1+
2
2
t
（t为参数），圆M的直角坐标方程为（x-a）2+（y-b）2=1，且圆M上的点到直线l的最小距离为1．
（1）求a-b的值；
（2）以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，圆N的极坐标方程为ρ=2cosθ，当a=1，b=1时，求圆M和圆N公共弦长．
已知P为抛物线y2=4x上一点，Q为圆C：（x+2）2+（y-2）2=1上一点，点P到直线l：x=-1的距离为d，则|PQ|+d的最小值为
 
．
在△ABC中，已知c2-a2=5b，3sinAcosC=cosAsinC，则b=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网