题目内容
(1)解不等式|2x-1|+|x+1|≥x+2;
(2)已知x,y,z为正实数,求3(x2+y2+z2)+
的最小值.
(2)已知x,y,z为正实数,求3(x2+y2+z2)+
| 2 |
| x+y+z |
考点:柯西不等式在函数极值中的应用,绝对值不等式的解法
专题:选作题,不等式
分析:(1)利用绝对值的几何意义,去掉绝对值,即可解不等式;
(2)由柯西不等式有(x2+y2+z2)(12+12+12)≥(x+y+z)2,即可求3(x2+y2+z2)+
的最小值.
(2)由柯西不等式有(x2+y2+z2)(12+12+12)≥(x+y+z)2,即可求3(x2+y2+z2)+
| 2 |
| x+y+z |
解答:
解:(1)
⇒x≥1或
⇒-1≤x≤0
或
⇒x<-1,
综上所解得原不等式的解集为{x|x≤0或x≥1};…5分
(2)由柯西不等式有(x2+y2+z2)(12+12+12)≥(x+y+z)2
所以3(x2+y2+z2)+
≥(x+y+z)2+
=(x+y+z)2+
+
≥3
=3
当且仅当x=y=z且(x+y+z)2=
,即x=y=z=
时取等号.
故3(x2+y2+z2)+
的最小值为3…10分.
|
|
或
|
综上所解得原不等式的解集为{x|x≤0或x≥1};…5分
(2)由柯西不等式有(x2+y2+z2)(12+12+12)≥(x+y+z)2
所以3(x2+y2+z2)+
| 2 |
| x+y+z |
| 2 |
| x+y+z |
| 1 |
| x+y+z |
| 1 |
| x+y+z |
| 3 | 1 |
当且仅当x=y=z且(x+y+z)2=
| 1 |
| x+y+z |
| 1 |
| 3 |
故3(x2+y2+z2)+
| 2 |
| x+y+z |
点评:本题主要考查了绝对值不等式的解法,以及柯西不等式的应用,解题的关键是利用(x2+y2+z2)(12+12+12)≥(x+y+z)2进行解题,属于中档题.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
已知向量
=(2,-1),
=(-2,3),则
-2
=( )
| a |
| b |
| a |
| b |
| A、(-6,7) |
| B、(-2,5) |
| C、(0,-2) |
| D、(6,-7) |
(
-
)8二项展开式中的常数项为( )
| 3 | x |
| 2 |
| x |
| A、112 | B、-112 |
| C、56 | D、-56 |
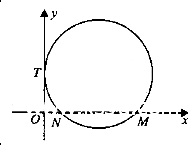 如图,已知圆C与y轴相切于点T(0,2),与x轴正半轴相交于两点M,N(点M必在点N的右侧),且|MN|=3,己知椭圆D:
如图,已知圆C与y轴相切于点T(0,2),与x轴正半轴相交于两点M,N(点M必在点N的右侧),且|MN|=3,己知椭圆D: