题目内容
在平行四边形ABCD中，|
|=1，|
|=2，|2
-
|=
，
（Ⅰ）求∠BAD；
（Ⅱ）若M，N分别是边BC，CD上的点，且满足
=
，求
•
的取值范围．
| AD |
| AB |
| AB |
| AD |
| 13 |
（Ⅰ）求∠BAD；
（Ⅱ）若M，N分别是边BC，CD上的点，且满足
|
| ||
|
|
|
| ||
|
|
| AM |
| AN |
考点：平面向量数量积的运算,向量的模
专题：平面向量及应用
分析：（Ⅰ）首先，根据|2
-
|=
，得到|2
-
|2=13，然后，借助于数量积的运算性质求解；
（Ⅱ）直接构造向量关系式，
•
=（
+
）•（
）=
=-（
+1）2+6，然后，结合二次函数的知识求解最值．
| AB |
| AD |
| 13 |
| AB |
| AD |
（Ⅱ）直接构造向量关系式，
| AM |
| AN |
| a |
| 1 |
| m |
| b |
| m-1 |
| m |
| b |
| 5m2-2m-1 |
| m2 |
| 1 |
| m |
解答：
解：（Ⅰ）∵|
|=1，|
|=2，|2
-
|=
，
∴|2
-
|2=13，
∴4|
|2-4|
||
|cos∠BAD+|
|2=13，
∴cos∠BAD=
，
∵∠BAD∈[0，π]，
∴∠BAD=
．
（Ⅱ）建立如图所示的直角坐标系，则B（2，0），A（0，0），
D（
，
），设
=
=λ，λ∈[0，1]，
M（2+
，
），N（
-2λ，
），
所以
•
=（2+
，
）•（
-2λ，
）=-λ2-2λ+5，
因为λ∈[0，1]，二次函数的对称轴为：λ=-1，
所以λ∈[0，1]时，-λ2-2λ+5∈[2，5]．
∴求
•
的取值范围[2，5]
| AD |
| AB |
| AB |
| AD |
| 13 |
∴|2
| AB |
| AD |
∴4|
| AB |
| AB |
| AD |
| AD |
∴cos∠BAD=
| 1 |
| 2 |
∵∠BAD∈[0，π]，
∴∠BAD=
| π |
| 3 |
（Ⅱ）建立如图所示的直角坐标系，则B（2，0），A（0，0），
D（
| 1 |
| 2 |
| ||
| 2 |
|
| ||
|
|
|
| ||
|
|
M（2+
| λ |
| 2 |
| ||
| 2 |
| 5 |
| 2 |
| ||
| 2 |
所以
| AM |
| AN |
| λ |
| 2 |
| ||
| 2 |
| 5 |
| 2 |
| ||
| 2 |
因为λ∈[0，1]，二次函数的对称轴为：λ=-1，
所以λ∈[0，1]时，-λ2-2λ+5∈[2，5]．
∴求
| AM |
| AN |
点评：本题重点考查了平面向量的基本运算，二次函数的图象与性质等知识，属于中档题．
练习册系列答案
相关题目
已知棱长为1的正方体ABCD-A1B1C1D1中，P，Q是面对角线A1C1上的两个不同动点．则以下结论不成立的是（ ）
| A、存在P，Q两点，使BP⊥DQ |
| B、存在P，Q两点，使BP，DQ与直线B1C都成45°的角 |
| C、若|PQ|=1，则四面体BDPQ的体积一定是定值 |
| D、若|PQ|=1，则四面体BDPQ在该正方体六个面上的正投影的面积的和为定值 |
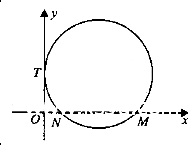如图，已知圆C与y轴相切于点T（0，2），与x轴正半轴相交于两点M，N（点M必在点N的右侧），且|MN|=3，己知椭圆D：