题目内容
若实数x，y满足
且z=x+2y的最小值为4，则实数m的值为 ．
|
考点：简单线性规划
专题：不等式的解法及应用
分析：作出不等式组对应的平面区域，利用z=x+2y的最小值为4，即可确定m的值．
解答：
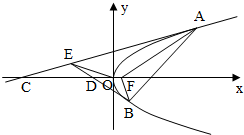
解：作出不等式组对应的平面区域如图：
∵z=x+2y的最小值为4，
∴x+2y=4，
且平面区域在直线x+2y=4的上方，
由图象可知当z=x+2y过x-2y=0与y=-x+m的交点时，z取得最小值．
由
，解得
，即A（2，1），
此时1=-2+m，解得m=3，
故答案为：3．
∵z=x+2y的最小值为4，
∴x+2y=4，
且平面区域在直线x+2y=4的上方，
由图象可知当z=x+2y过x-2y=0与y=-x+m的交点时，z取得最小值．
由
|
|
此时1=-2+m，解得m=3，
故答案为：3．
点评：本题主要考查线性规划的应用，利用数形结合是解决本题的关键．
练习册系列答案
相关题目
在复平面内，复数
对应的点位于（ ）
| 2-i |
| i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
若集合M={x|y=
}，N={y|y=x2-2，x∈R}，则M∩N=（ ）
| x |
| A、[0，+∞） |
| B、[-2，+∞） |
| C、∅ |
| D、[-2，0） |
设抛物线Γ：y2=2px（p＞0）过点（t，