Question

设抛物线Γ：y²=2px（p＞0）过点（t，

2t

）（t是大于0的常数）．
（Ⅰ）求抛物线Γ的方程；
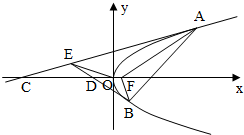
（Ⅱ）若F是抛物线Γ的焦点，斜率为1的直线交抛物线Γ于A，B两点，x轴负半轴上的点C，D满足|FA|=|FC|，|FD|=|FB|，直线AC，BD相交于点E，当

S△AEF•S△BEF

S△ABF2

=

5

8

时，求直线AB的方程．

Answer 1

考点：抛物线的标准方程

专题：综合题,圆锥曲线的定义、性质与方程

分析：（Ⅰ）根据抛物线R：y²=2px（p＞0）过点（t，

2t

），求出p，即可得出抛物线Γ的方程；
（Ⅱ）设直线AB的方程为y=x-m代入抛物线方程，可得x²-2（m+1）x+m²=0，求出直线AC、BD的方程，可得E的坐标，求出相应三角形的面积，利用

S△AEF•S△BEF

S△ABF2

=

5

8

，即可求直线AB的方程．

解答： 解：（Ⅰ）∵抛物线R：y²=2px（p＞0）过点（t，

2t

），
∴2t=2pt，
∴p=1，
∴抛物线R的方程为y²=2x；
（Ⅱ）设直线AB的方程为y=x-m，A（x₁，y₁），B（x₂，y₂），
直线方程代入抛物线方程，可得x²-2（m+1）x+m²=0，
△=8m+4＞0，∴m＞-

1

2

，
x₁+x₂=2（m+1），x₁x₂=m²，
∴|x₁-x₂|=2

2m+1

，y₁+y₂=2，y₁y₂=-2m，
∵|FA|=|FC|，∴x_C=-x₁，
∴k_AC=

y1

2x1

=

1

y1

，直线AC的方程为x-y₁y+x₁=0，①
同理直线BD的方程为x-y₂y+x₂=0，②
由①②可得E（-m，1），
∴S_△AEF=

1

2

（

1

2

+x₁）（y₁-1），S_△BEF=

1

2

（

1

2

+x₂）（y₂-1），
∴S_△AEFS_△BEF=

1

16

[（2m+1）²+4]（2m+1），
在△ABF中，|AB|=

2

|x₁-x₂|=2

2

2m+1

，
F到直线AB的距离为d=

|2m-1|

2 2

，
∴S_△ABF=

1

2

2m+1

|2m-1|
∵

S△AEF•S△BEF

S△ABF2

=

5

8

，
∴

1

4

•

(2m+1)2+4

(2m-1)2

=

5

8

，
∴m=

5

2

或m=-

1

6

，
∴直线AB的方程为y=x-

5

2

或y=x+

1

6

．

点评：本题考查抛物线的方程，考查直线与抛物线的位置关系，考查三角形面积的计算，考查学生分析解决问题的能力，属于中档题．