题目内容
根据下列各题中的条件,求相应的等差数列{an}未知数:
(1)a1=
,d=-
,Sn=-5,求n及an;
(2)d=2,n=15,an=-10,求a1及Sn.
(1)a1=
| 5 |
| 6 |
| 1 |
| 6 |
(2)d=2,n=15,an=-10,求a1及Sn.
考点:等差数列的性质
专题:等差数列与等比数列
分析:根据等差数列的性质,求出首项和公差,即可求它的通项公式an
解答:
解:(1)∵Sn=
n+
×(-
)=-5,
∴n2-11n-60=0,解得n=15或n=-4(舍),
则an=a15=
-14×
=-
;
(2)∵an=a1+14×2=-10,
∴a1=-38,Sn=15×(-38)+
×2=-360.
| 5 |
| 6 |
| n(n-1) |
| 2 |
| 1 |
| 6 |
∴n2-11n-60=0,解得n=15或n=-4(舍),
则an=a15=
| 5 |
| 6 |
| 1 |
| 6 |
| 3 |
| 2 |
(2)∵an=a1+14×2=-10,
∴a1=-38,Sn=15×(-38)+
| 15×14 |
| 2 |
点评:本题主要考查等差数列的通项公式和前n项和的计算,根据等差数列的定义是解决本题的关键,比较基础.

练习册系列答案
相关题目
若x∈R,则“x<
”是“sinx>0”的( )
| π |
| 2 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
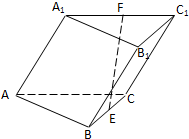 如图,斜三棱柱ABC-A1B1C1的侧棱长为
如图,斜三棱柱ABC-A1B1C1的侧棱长为