题目内容
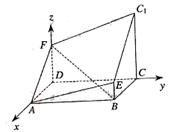
如图所示的多面体是由底面为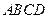 的长方体被截面
的长方体被截面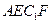 所截面而得到的,其中
所截面而得到的,其中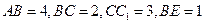 .
.
(Ⅰ)求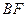 的长;
的长;
(Ⅱ)求二面角E-FC1-C的余弦值.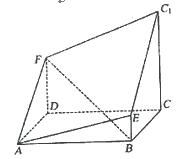
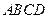 的长方体被截面
的长方体被截面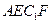 所截面而得到的,其中
所截面而得到的,其中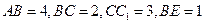 .
.(Ⅰ)求
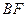 的长;
的长;(Ⅱ)求二面角E-FC1-C的余弦值.

(Ⅰ)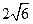
(Ⅱ)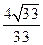
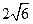
(Ⅱ)
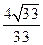
(I)建立如图所示的空间直角坐标系,则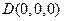 ,
,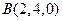
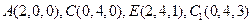 设
设 .
.
∵ 为平行四边形,
为平行四边形,
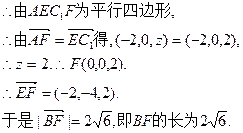
(II)设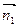 为平面
为平面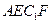 的法向量且
的法向量且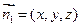
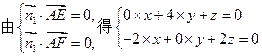

设二面角E-FC1-C为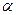 ,则
,则
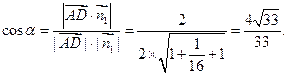
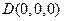 ,
,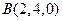
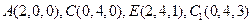 设
设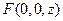 .
.
∵
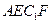 为平行四边形,
为平行四边形,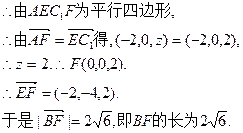
(II)设
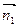 为平面
为平面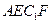 的法向量且
的法向量且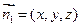
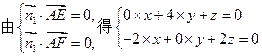

设二面角E-FC1-C为
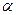 ,则
,则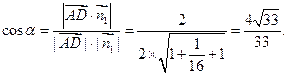

练习册系列答案
相关题目
 平面ACB1)作垂直于D1B的平面分别交过D1的三条棱于E、F、G.
平面ACB1)作垂直于D1B的平面分别交过D1的三条棱于E、F、G.
 中,
中, ,底面
,底面 为梯形,
为梯形, ,
, ,且
,且
 .(10分)
.(10分)
 ;
; 的余弦值.
的余弦值.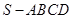 的底面是正方形,
的底面是正方形,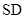 ⊥平面
⊥平面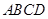 ,
,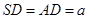 ,点E是SD上的点,且
,点E是SD上的点,且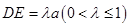 .
.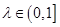 ,都有AC⊥BE;
,都有AC⊥BE;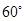 ,求
,求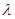 的值.
的值.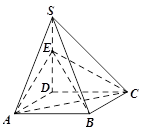
 的正方体
的正方体 中,
中, 、
、 分别是
分别是 、
、 的中点,求点
的中点,求点 到截面
到截面 的距离 .
的距离 . 两两垂直,
两两垂直, 是
是 的中点,
的中点, 是
是 的中点.
的中点. 的坐标;
的坐标; 与底面
与底面 所成的角的余弦值.
所成的角的余弦值.
 的长方体被截面
的长方体被截面 所截而得到的,其中
所截而得到的,其中 .
. ;
; 到平面
到平面



 的面积。
的面积。