题目内容
设p：实数x满足（x-3a）（x-a）＜0，其中a＞0，q：实数x满足
（1）当a=1，p且q为真时，求实数x的取值范围；
（2）若￢p是￢q的充分不必要条件，求实数a的取值范围．
|
（1）当a=1，p且q为真时，求实数x的取值范围；
（2）若￢p是￢q的充分不必要条件，求实数a的取值范围．
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：（1）当a=1，p且q为真时，则p，q同时为真，建立条件即可求实数x的取值范围；
（2）利用?p是?q的充分不必要条件，转化为q是p的充分不必要条件，建立条件关系即可求实数a的取值范围．
（2）利用?p是?q的充分不必要条件，转化为q是p的充分不必要条件，建立条件关系即可求实数a的取值范围．
解答：
解：（1）当a=1时，p：1＜x＜3，q：2＜x≤3，
∵p且q为真，
∴p，q同时为真，即x满足
，
即2＜x＜3．
（2）∵￢p是￢q的充分不必要条件知，
∴q是p的充分不必要条件，
由p知，即A={x|a＜x＜3a，a＞0}，
由q知，B={x|2＜x≤3}
∴B?A，
∴a≤2且3＜3a，解得1＜a≤2
即实数a的取值范围是（1，2]．
∵p且q为真，
∴p，q同时为真，即x满足
|
即2＜x＜3．
（2）∵￢p是￢q的充分不必要条件知，
∴q是p的充分不必要条件，
由p知，即A={x|a＜x＜3a，a＞0}，
由q知，B={x|2＜x≤3}
∴B?A，
∴a≤2且3＜3a，解得1＜a≤2
即实数a的取值范围是（1，2]．
点评：本题主要考查充分条件和必要条件的应用，利用复合命题之间的关系是解决本题的关键．
练习册系列答案
应用题作业本系列答案
相关题目
已知一个三棱柱的三视图如图所示，则该三棱柱的表面积为（ ）
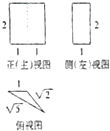
A、4
| ||||||
B、2
| ||||||
C、
| ||||||
D、2
|
设函数f（x）=
，g（x）=x2f（x-1），则函数g（x）的递减区间是（ ）
|
| A、（0，1] |
| B、（0，1） |
| C、（-∞，0） |
| D、（0，+∞） |