��Ŀ����
��֪����g��x��=��
��x��
��1�������x�ĺ���y=[g��x��]2-2ag��x��+3��a��3������x��[-1��1]ʱ����Сֵh��a����
��2�����ǰ�ͬʱ���������������ʵĺ�����Ϊ����г���������ٺ������������������ǵ����������������������ں����Ķ������ڴ�������[p��q]��p��q����ʹ�ú���������[p��q]�ϵ�ֵ��Ϊ[p2��q2]��
�����жϣ�1����h��x���Ƿ�Ϊ����г�����������ǣ����p��q��ֵ���ϵʽ�������ǣ���˵�����ɣ�
����������x���y=
+t��x��1���ǡ���г����������ʵ��t��ȡֵ��Χ��
| 1 |
| 3 |
��1�������x�ĺ���y=[g��x��]2-2ag��x��+3��a��3������x��[-1��1]ʱ����Сֵh��a����
��2�����ǰ�ͬʱ���������������ʵĺ�����Ϊ����г���������ٺ������������������ǵ����������������������ں����Ķ������ڴ�������[p��q]��p��q����ʹ�ú���������[p��q]�ϵ�ֵ��Ϊ[p2��q2]��
�����жϣ�1����h��x���Ƿ�Ϊ����г�����������ǣ����p��q��ֵ���ϵʽ�������ǣ���˵�����ɣ�
����������x���y=
| x2-1 |
���㣺ָ��������ͼ��������,ָ�������ۺ���
ר�⣺���������ʼ�Ӧ��
��������1����f��x�����ɹ���x�ķ��̣����x����x��y�����õ�g��x����
��2��ͨ����Ԫ��������ת��Ϊ����t�Ķ��κ���������Գ��ᣬͨ���ԶԳ���������λ�ù�ϵ�����ۣ������Сֵg��a����
���ݺ�г�����Ķ��壬�г������飬���p��q�����������
�������¶��壬���첻��ʽ�飬��ü���
��2��ͨ����Ԫ��������ת��Ϊ����t�Ķ��κ���������Գ��ᣬͨ���ԶԳ���������λ�ù�ϵ�����ۣ������Сֵg��a����
���ݺ�г�����Ķ��壬�г������飬���p��q�����������
�������¶��壬���첻��ʽ�飬��ü���
���
�⣺��1������֪�ã�y-2a(
)x+3����a��3������x��[-1��1]
��t=��
��x����t��[
��3]��y=t2-2a+3��
1����a��
ʱ��h��a��=y=��
��=
-
+3=
-
��
2����
��a��3ʱ��g��a��=y��a��=3-a2��
��h��a��=
��
��2�����ԣ�2����h��x��=
����֪g��x���ڣ�-�ޣ�3]��Ϊ��������
1����p��q��
ʱ��h��x���ݼ������ǡ���г��������
��
��
��p+q=
��p��q��
ì�ܣ�
2����
��p��q��3ʱ����
����-p2+q2=q2-p2��ȣ�
��ʱ�������⣬����������p��q���ڣ�
3����p��
��
��q��3����
����
��
��28-6p=9��3-p2����
��9p2-6p+1=0��
��p=
��p��
ì�ܣ���p��q���㣺
����y=
+t��x��1������[1��+�ޣ��ϵ������ɡ���г�������Ķ���֪���ú����ڶ�����[1��+�ޣ��ڣ���������[p��q]����p��q����
ʹ�øú�����[p��q]���ϵ�ֵ��Ϊ[p2��q2]������p��1��
��
��p2��q2����
+t=x�Ķ�ʵ����
������x2-��2t+1��x+t2+1=0��[1��+�ޣ��ϴ����������ȵ�ʵ������x��t�������
��u��x��=x2-��2t+1��x+t2+1��
��
��
��
��
���
��t��1
��ʵ��t��ȡֵ��Χ��
��1]
| 1 |
| 3 |
��t=��
| 1 |
| 3 |
| 1 |
| 3 |
1����a��
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 9 |
| 2a |
| 3 |
| 28 |
| 9 |
| 2a |
| 3 |
2����
| 1 |
| 3 |
��h��a��=
|
��2�����ԣ�2����h��x��=
|
1����p��q��
| 1 |
| 3 |
��
|
��p+q=
| 2 |
| 3 |
| 1 |
| 3 |
2����
| 1 |
| 3 |
|
��ʱ�������⣬����������p��q���ڣ�
3����p��
| 1 |
| 3 |
| 1 |
| 3 |
|
|
��28-6p=9��3-p2����
��9p2-6p+1=0��
��p=
| 1 |
| 3 |
| 1 |
| 3 |
|
����y=
| x2-1 |
ʹ�øú�����[p��q]���ϵ�ֵ��Ϊ[p2��q2]������p��1��
|
��p2��q2����
| x-1 |
������x2-��2t+1��x+t2+1=0��[1��+�ޣ��ϴ����������ȵ�ʵ������x��t�������
��u��x��=x2-��2t+1��x+t2+1��
��
|
��
|
���
| 3 |
| 4 |
��ʵ��t��ȡֵ��Χ��
| 3 |
| 4 |
���������⿼���¶����⣬�ؼ����������е��¶��壬��ֶκ����ĺ���ֵ�ؼ����жϳ��Ա��������ķ�Χ����������

��ϰ��ϵ�д�
 ���������������Բ��������ϵ�д�
���������������Բ��������ϵ�д�
�����Ŀ
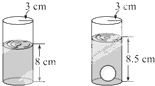 һ��Բ���εIJ���ƿ���ڰ뾶Ϊ3cm��ƿ����װ��ˮ��Ϊ8cm����һ��������ȫ����ˮ�У�ƿ��ˮ�ĸ߶�������8.5cm�������İ뾶Ϊ��������
һ��Բ���εIJ���ƿ���ڰ뾶Ϊ3cm��ƿ����װ��ˮ��Ϊ8cm����һ��������ȫ����ˮ�У�ƿ��ˮ�ĸ߶�������8.5cm�������İ뾶Ϊ��������| A��1 cm |
| B��1.2 cm |
| C��1.5 cm |
| D��2 cm |
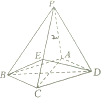 ��ͼ������P-AB-CD�У�����ABCDΪ���Σ�PA�͵���ABCD��AC=2
��ͼ������P-AB-CD�У�����ABCDΪ���Σ�PA�͵���ABCD��AC=2