题目内容
18.现有四个函数:①y=x•sinx,②y=x•cosx,③y=x•|cosx|,④y=x•2x 的部分图象如图,但顺序被打乱,则按照从左到右将图象对应的函数序号正确的排列是①④②③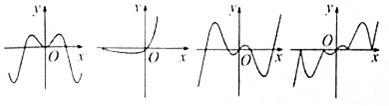
分析 依据函数的性质与图象的图象对应来确定函数与图象之间的对应关系,对函数的解析式研究发现,四个函数中有一个是偶函数,有两个是奇函数,还有一个是指数型递增较快的函数,由这些特征接合图象上的某些特殊点判断即可.
解答 解:研究发现①是一个偶函数,其图象关于y轴对称,故它对应第一个图象
②③都是奇函数,但②在y轴的右侧图象在x轴上方与下方都存在,而③在y轴右侧图象只存在于x轴上方,故②对应第三个图象,③对应第四个图象,④与第二个图象对应,易判断.
故按照从左到右与图象对应的函数序号①④②③
故答案为:①④②③
点评 本题考点是正弦函数的图象,考查了函数图象及函数图象变化的特点,解决此类问题有借助两个方面的知识进行研究,一是函数的性质,二是函数值在某些点的符号即图象上某些特殊点在坐标系中的确切位置.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.抛物线x2=$\frac{1}{4}$y上的一点M到焦点的距离为1,则点M到x轴的距离是( )
| A. | $\frac{17}{16}$ | B. | $\frac{15}{16}$ | C. | 1 | D. | $\frac{7}{8}$ |
13.化简$\frac{cos2α}{{4{{sin}^2}(\frac{π}{4}+α)tan(\frac{π}{4}-α)}}$=( )
| A. | cosα | B. | sinα | C. | 1 | D. | $\frac{1}{2}$ |
3.若全集U={1,2,3,4,5},M={1,4},N={2,3},则(∁UM)∩N=( )
| A. | {3,5} | B. | {2,3,5} | C. | {2,5} | D. | {2,3} |
8.直线x-y=0与圆x2+y2=1的位置关系是( )
| A. | 相切 | B. | 相离 | ||
| C. | 相交且直线过圆心 | D. | 相交且直线不过圆心 |
