题目内容
 为了了解调研高一年级新学生的智力水平,某校按l 0%的比例对700名高一学生按性别分别进行“智力评分”抽样检查,测得“智力评分”的频数分布表如表l,表2.
为了了解调研高一年级新学生的智力水平,某校按l 0%的比例对700名高一学生按性别分别进行“智力评分”抽样检查,测得“智力评分”的频数分布表如表l,表2.表1:男生“智力评分”频数分布表
| 智力评分 | [160,165) | [165,170) | [170,175) | [175,180) | [180,185) | [185,190) |
| 频数 | 2 | 5 | 14 | 13 | 4 | 2 |
| 智力评分 | [150,155) | [155,160) | [160,165) | [165,170) | [170,175) | [175,180) |
| 频数 | 1 | 7 | 12 | 6 | 3 | 1 |
(Ⅱ)估计该校学生“智力评分”在[165,180)之间的概率;
(Ⅲ)从样本中“智力评分”在[180,190)的男生中任选2人,求至少有1人“智力评分”在[185,190)之间的概率.
考点:古典概型及其概率计算公式,频率分布直方图
专题:概率与统计
分析:(Ⅰ)根据频率分布直方图画法即可解答;
(Ⅱ)根据频率分布直方图查找到[165,180)之间人找到数,在利用概率公式即可求得;
(Ⅲ)一一列举出所有满足条件的基本事件,找到至少有1人“智力评分”在[180,190)的基本事件,利用古典概型的概率公式求得.
(Ⅱ)根据频率分布直方图查找到[165,180)之间人找到数,在利用概率公式即可求得;
(Ⅲ)一一列举出所有满足条件的基本事件,找到至少有1人“智力评分”在[180,190)的基本事件,利用古典概型的概率公式求得.
解答:
解:(Ⅰ)样本中男生人数是40,由抽样比例是10%可得高一的男生人数是400,
男生的频率分布直方图如图所示
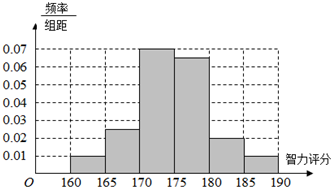
(Ⅱ)由表1和表2知,样本中“智力评分”在[165,180)中的人数是5+14+13+6+3+1=42,样本的容量是70,
所以样本中学生“智力评分”在[165,180)之间的频率f=
=
,
由f估计学生“智力评分”在[165,180)之间的概率是P=
(Ⅲ)样本中智力评分”在[180,185)之间的有4人,设其编号是1,2,3,4,样本中“智力评分”在[185,190)间的男生有2人,
设其编号为5,6,从中任取2人的结果总数是12,13,14,15,16,23,24,25,26,34,35,36,45,46,56共15种,
至少有1人“智力评分”在[185,190)间的有9种,
因此所求概率是P=
=
男生的频率分布直方图如图所示

(Ⅱ)由表1和表2知,样本中“智力评分”在[165,180)中的人数是5+14+13+6+3+1=42,样本的容量是70,
所以样本中学生“智力评分”在[165,180)之间的频率f=
| 42 |
| 70 |
| 3 |
| 5 |
由f估计学生“智力评分”在[165,180)之间的概率是P=
| 3 |
| 5 |
(Ⅲ)样本中智力评分”在[180,185)之间的有4人,设其编号是1,2,3,4,样本中“智力评分”在[185,190)间的男生有2人,
设其编号为5,6,从中任取2人的结果总数是12,13,14,15,16,23,24,25,26,34,35,36,45,46,56共15种,
至少有1人“智力评分”在[185,190)间的有9种,
因此所求概率是P=
| 9 |
| 15 |
| 3 |
| 5 |
点评:本题主要考查了频率分布直方图,以及古典概型的概率的求法.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
等差数列{an}中,已知a1+a3=6,a5+a7=14,则a20+a22=( )
| A、44 | B、56 | C、42 | D、40 |
在△ABC中,角A、B、C所对边长分别为a,b,c,若a2+b2=3c2,则cosC的最小值为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列关于向量若
,
的命题中,错误命题的是( )
| a |
| b |
A、若
| ||||||||||
B、若k∈R,k
| ||||||||||
C、若|
| ||||||||||
D、若
|