题目内容
9.点F为抛物线y2=2px的焦点,点P在y轴上,PF交抛物线于点Q,且|PQ|=|QF|=1,则p等于$\frac{4}{3}$.分析 根据抛物线的焦点弦公式,求得x0=1-$\frac{p}{2}$,由丨OQ丨=1,代入即可求得p的值.
解答 解:设P(x0,y0),y02=2px0,抛物线的焦点坐标($\frac{p}{2}$,0),准线方程x=-$\frac{p}{2}$,
由抛物线的焦点弦公式可知:|QF|=x0+$\frac{p}{2}$=1,则x0=1-$\frac{p}{2}$,
由直角三角形的性质,丨OQ丨=|PQ|=|QF|=1,即x02+y02=1,
即(1-$\frac{p}{2}$)2+2px0=1,解得:p=$\frac{4}{3}$.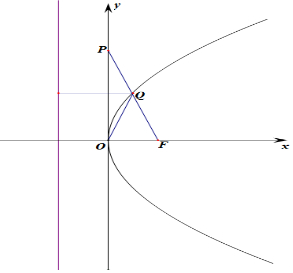
故答案为:$\frac{4}{3}$.
点评 本题考查抛物线的性质,抛物线的焦点弦公式,考查数形结合思想,属于中档题.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
17.集合A={x|x≥0},B={x|x2-1<0},则A∩B=( )
| A. | (-1,0] | B. | [0,1] | C. | (-1,1) | D. | [0,1) |
14.将3个不同的小球放入4个不同的盒子中,则不同的放法种数有( )
| A. | 12 | B. | 14 | C. | 64 | D. | 81 |
19.某小区现有住房的面积为a平方米,在改造过程中政府决定每年拆除b平方米旧住房,同时按当店住房面积的10%建设新住房,则n年后该小区的住房面积为( )
| A. | a•1.1n-nb | B. | a•1.1n-10b(1.1n-1) | ||
| C. | n(1.1a-1) | D. | (a-b)1.1n |
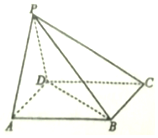 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD是正三角形,且平面PAD⊥平面ABCD.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD是正三角形,且平面PAD⊥平面ABCD.