已知f(x)是定义在R上的函数.f′(x)是其导函数.若满足f′=-f的图象可能是( )A．B．C．D．题目和参考答案——青夏教育精英家教网—

题目内容

4．已知f（x）是定义在R上的函数，f′（x）是其导函数，若满足f′（-x）=f′（x），f（x+2）=-f（x），则函数y=f（x）的图象可能是（　　）

	A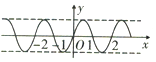．			B．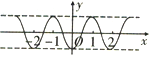
	C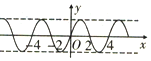．			D．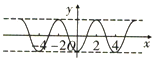

分析利用排除法，即可得出函数的图象．

解答解：由f（x+2）=-f（x），有$f（{\frac{3}{2}}）=-f（{-\frac{1}{2}}）$，排除A；同理f（1）=-f（-1），排除B；
由f'（-x）=f'（x），有f'（-1）=f'（1），即函数图象在x=1和x=-1处的切线平行，排除D，
故选C．

点评本题考查了函数的图象以及函数单调性与导数的关系，本题要有一定的识图能力．

练习册系列答案

浙江新课程三维目标测评课时特训系列答案

15．有一算法流程图如图所示，该算法解决的是（　　）

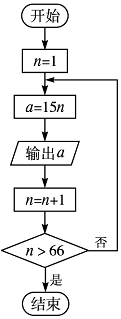
	A．	输出不大于990且能被15整除的所有正整数
	B．	输出不大于66且能被15整除的所有正整数
	C．	输出67
	D．	输出能被15整除且大于66的正整数

12．已知数列{a_n}的前n项和为S_n，且S_n=n²+2n，
（1）求数列{a_n}的通项公式；
（2）若数列{c_n}满足条件：${c_{n+1}}={a_{c_n}}+{2^n}$，又c₁=3，是否存在实数λ，使得数列$\left\{{\frac{{{c_n}+λ}}{2^n}}\right\}$为等差数列？

19．函数$y=sin（{x+\frac{π}{3}}）$的图象（　　）

	A．	对称关于点$（\frac{π}{6}，0）$对称		B．	关于直线$x=\frac{π}{6}$
	C．	关于y轴对称		D．	关于原点对称

9．点F为抛物线y²=2px的焦点，点P在y轴上，PF交抛物线于点Q，且|PQ|=|QF|=1，则p等于$\frac{4}{3}$．

16．在数列{a_n}中，${a_1}=1，{\;}_{\;}{a_{n+1}}=\frac{{3{a_n}}}{{3+{a_n}}}{\;}_{\;}（n∈{N^+}）$，
（1）写出这个数列的前4项，并猜想这个数列的通项公式；
（2）证明这个数列的通项公式．

13．已知f（x）的定义域为（0，+∞），f′（x）为f（x）的导函数，且满足f（x）＞-xf′（x），则不等式f（x+1）＞（x-1）f（x²-1）的解集是（　　）

14．在函数：①y=cos|x|②y=|sinx|③$y=cos（2x+\frac{π}{6}）$④$y=tan（2x-\frac{π}{4}）$中，最小正周期为π的所有函数为（　　）

试题分类