Question

18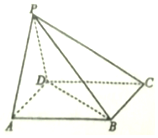．如图，在四棱锥P-ABCD中，底面ABCD是正方形，侧面PAD是正三角形，且平面PAD⊥平面ABCD．
（1）求证：AB⊥平面PAD；
（2）求直线PC与底面ABCD所成角的余弦值．

Answer 1

分析 （1）建立空间直角坐标系D-xyz，由$\overrightarrow{AB}•\overrightarrow{PA}=0$⇒PA⊥AB．由AB⊥AD，即可得到AB⊥平面PAD；
（2）取AD的中点F，连结PF，CF，可得PF⊥平面BCD，即CF是PC在平面ABCD上的射影，可得∠PCF是直线PC与底面ABCD所成的角，利用向量求解

解答 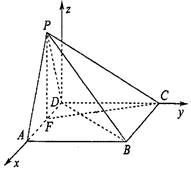（1）证明：建立空间直角坐标系D-xyz，
如图不妨设A（1，0，0）则B（1，1，0），P（$\frac{1}{2}，0，\frac{{\sqrt{3}}}{2}）$$\overrightarrow{AB}=（0，1，0），\overrightarrow{PA}=（\frac{1}{2}，0，-\frac{{\sqrt{3}}}{2}）$…（2分）
由$\overrightarrow{AB}•\overrightarrow{PA}=0$⇒PA⊥AB．
由AB⊥AD，∴AB⊥平面PAD   …（6分）
（2）解：取AD的中点F，连结PF，CF
∵平面PAD⊥平面ABCD，且PF⊥AD，
∴PF⊥平面BCD                        …（5分）
∴CF是PC在平面ABCD上的射影，
∴所以∠PCF是直线PC与底面ABCD所成的角…（7分）
易知C（0，1，0），F（$\frac{1}{2}，0，0）$，∴$\overrightarrow{CP}=（\frac{1}{2}，-1，\frac{{\sqrt{3}}}{2}），\overrightarrow{CP}=（\frac{1}{2}，-1，0）$
∴$cos＜\overrightarrow{CP}，\overrightarrow{CF}＞=\frac{{\overrightarrow{CP}•\overrightarrow{CF}}}{{|{\overrightarrow{CP}}|•|{\overrightarrow{CF}}|}}=\frac{{\sqrt{10}}}{4}$
∴直线PC与底面ABCD所成角的余弦值$\frac{{\sqrt{10}}}{4}$…（12分）

点评 本题考查了向量法证明线面垂直、向量法求线面角，属于中档题．