题目内容
已知点A(1,0),B(2,
),C(m,2m),若直线AC的倾斜角是直线AB的倾斜角的2倍,求m的值 .
| 3 |
考点:直线的倾斜角
专题:直线与圆
分析:由点AB的坐标,求出直线AB的斜率,进而求出直线AB的倾斜角,结合直线AC的倾斜角是直线AB的倾斜角的2倍,可得直线AC的倾斜角,代入斜率公式,构造关于m的方程,解方程可得答案.
解答:
解:∵点A(1,0),B(2,
),
∴kAB=
=
,
即直线AB的倾斜角为60°,
又∵直线AC的倾斜角是直线AB的倾斜角的2倍,
∴直线AC的倾斜角是120°,
故kAC=
=tan120°=-
,
解得:m=2
-3,
故答案为:2
-3
| 3 |
∴kAB=
| ||
| 2-1 |
| 3 |
即直线AB的倾斜角为60°,
又∵直线AC的倾斜角是直线AB的倾斜角的2倍,
∴直线AC的倾斜角是120°,
故kAC=
| 2m |
| m-1 |
| 3 |
解得:m=2
| 3 |
故答案为:2
| 3 |
点评:本题考查的知识点是直线的倾斜角,斜率公式,难度不大,属于基础题.

练习册系列答案
相关题目
已知平面向量
=(1,2),
=(2,-m)且
⊥
,则3
+2
=( )
| a |
| b |
| a |
| b |
| a |
| b |
| A、(-4,-10) |
| B、(-4,7) |
| C、(-3,-6) |
| D、(7,4) |
在等差数列{an}中,有a4+a8=a5+a7,类比上述性质,在等比数列{bn}中,有( )
| A、b4+b8=b5+b7 |
| B、b4b8=b5b7 |
| C、b4b5=b7b8 |
| D、b4b7=b5b8 |
若直线AB的斜率是
,将直线AB绕A点按逆时针方向旋转45°后,所得直线的倾斜角是( )
| 3 |
| A、105° | B、15° |
| C、75° | D、120° |
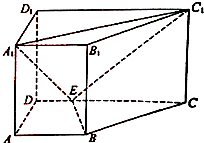 如图,直四棱柱中ABCD-A1B1C1D1中,AB∥CD,AD⊥AB,AB=3,AD=1,AA1=2,CD=4,E是CD中点.
如图,直四棱柱中ABCD-A1B1C1D1中,AB∥CD,AD⊥AB,AB=3,AD=1,AA1=2,CD=4,E是CD中点.