题目内容
已知一个算法的程序框图如图所示，当输出的结果为0时，输入的x的值为（ ）
| A、1 | B、-2 |
| C、1或-1 | D、1或-2 |
考点：程序框图
专题：算法和程序框图
分析：分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知：该程序的作用是计算并输出分段函数y=
的函数值．
|
解答：
解：分析程序中各变量、各语句的作用，
再根据流程图所示的顺序，可知：
该程序的作用是计算并输出分段函数y=
的函数值．
当x≥0时，若y=x2-1=0，则x=1，或x=-1（舍），
当x＜0时，若y=x2+4=0，无解
故输入的x的值为1，
故选：A
再根据流程图所示的顺序，可知：
该程序的作用是计算并输出分段函数y=
|
当x≥0时，若y=x2-1=0，则x=1，或x=-1（舍），
当x＜0时，若y=x2+4=0，无解
故输入的x的值为1，
故选：A
点评：算法是新课程中的新增加的内容，也必然是新高考中的一个热点，应高度重视．程序填空也是重要的考试题型，这种题考试的重点有：①分支的条件②循环的条件③变量的赋值④变量的输出．其中前两点考试的概率更大．此种题型的易忽略点是：不能准确理解流程图的含义而导致错误．
练习册系列答案
相关题目
把函数y=sin（2x+
）的图象向右平移
个单位，再把所得图象上各点的横坐标缩短到原来的
，则所得图象的函数解析式是（ ）
| π |
| 4 |
| π |
| 8 |
| 1 |
| 2 |
A、y=sin（4x+
| ||
B、y=sin（4x+
| ||
| C、y=sin4x | ||
| D、y=sinx |
已知向量
=（8+
x，x），
=（x+1，2），其中x＞0，若
∥
，则x的值为（ ）
| a |
| 1 |
| 2 |
| b |
| a |
| b |
| A、8 | B、4 | C、2 | D、0 |
一个平面封闭区域内任意两点距离的最大值称为该区域的“直径”，封闭区域边界曲线的长度与区域直径之比称为区域的“周率”，下面四个平面区域（阴影部分）的周率从左到右依次记为τ1，τ2，τ3，τ4，则下列关系中正确的为（ ）
| A、τ1＞τ4＞τ3 |
| B、τ3＞τ1＞τ2 |
| C、τ4＞τ2＞τ3 |
| D、τ3＞τ4＞τ1 |
下列各数中最小的数是（ ）
| A、85（9） |
| B、210（6） |
| C、1000（4） |
| D、111111（2） |
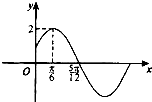已知函数f（x）=2sin（ωx+φ）（ω＞0，|φ|＜| π |
| 2 |
A、f（x）=2sin（
| ||||
B、f（x）=2sin（
| ||||
C、f（x）=2sin（2x-
| ||||
D、f（x）=2sin（2x+
|
若sinα，cosα是方程3x2+6mx+2m+1=0的两根，则实数m的值为（ ）
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
为了解72名学生的学习情况，采用系统抽样的方法，从中抽取容量为8的样本，则分段的间隔为（ ）
| A、9 | B、8 | C、10 | D、7 |