题目内容
从一箱产品中随机地抽取一件,设事件A={抽到一等品},事件B={抽到二等品},事件C={抽到三等品},且已知 P(A)=0.65,P(B)=0.2,P(C)=0.1.则事件“抽到的不是一等品”的概率为( )
| A、0.7 | B、0.65 |
| C、0.35 | D、0.3 |
考点:互斥事件的概率加法公式
专题:概率与统计
分析:根据对立事件的概率和为1,结合题意,即可求出结果来.
解答:
解:根据对立事件的概率和为1,得;
∵事件A={抽到一等品},且 P(A)=0.65,
∴事件“抽到的不是一等品”的概率为
P=1-P(A)=1-0.65=0.35.
故选:C.
∵事件A={抽到一等品},且 P(A)=0.65,
∴事件“抽到的不是一等品”的概率为
P=1-P(A)=1-0.65=0.35.
故选:C.
点评:本题考查了求互斥事件与对立事件的概率的应用问题,是基础题目.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
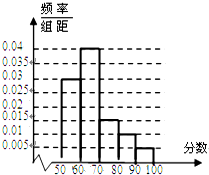 在某中学举行的环保知识竞赛中,将三个年级参赛的学生的成绩进行整理后分为5组,绘制出如图所示的频率分布直方图,图中从左到右依次为第一、第二、第三、第四、第五小组,已知第二小组的频数是40,则成绩在80~100分的学生人数是( )
在某中学举行的环保知识竞赛中,将三个年级参赛的学生的成绩进行整理后分为5组,绘制出如图所示的频率分布直方图,图中从左到右依次为第一、第二、第三、第四、第五小组,已知第二小组的频数是40,则成绩在80~100分的学生人数是( )| A、15 | B、18 | C、20 | D、25 |
用秦九韶算法计算多项式f(x)=2x5-3x4+7x3-9x2+4x-10在x=2时的值时,V3的值为( )
| A、34 | B、22 | C、9 | D、1 |
 设四棱锥P-ABCD中,底面ABCD是边长为1的正方形,且PA⊥面ABCD.
设四棱锥P-ABCD中,底面ABCD是边长为1的正方形,且PA⊥面ABCD.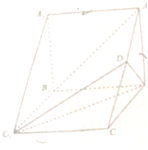 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,△ABC是等边三角形,D为AC的中点,AA1=AB=2.
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,△ABC是等边三角形,D为AC的中点,AA1=AB=2.