题目内容
17.已知点A(0,4),B(-2,0),则线段AB中点C的坐标是( )| A. | (-2,4) | B. | (-1,2) | C. | (1,2) | D. | (2,4) |
分析 设线段AB中点C的坐标为(x,y),由A、B的坐标可得x、y的值,即可得答案.
解答 解:设线段AB中点C的坐标为(x,y),
而点A(0,4),B(-2,0),则有x=$\frac{0+(-2)}{2}$=-1,y=$\frac{4+0}{2}$=2,
即C的坐标为(-1,2),
故选:B.
点评 本题考查中点坐标的计算,掌握中点坐标公式是解题的关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
7.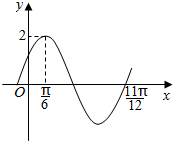 已知函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,丨φ丨<$\frac{π}{2}$)的部分图象如图所示,则f(x)的解析式为( )
已知函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,丨φ丨<$\frac{π}{2}$)的部分图象如图所示,则f(x)的解析式为( )
 已知函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,丨φ丨<$\frac{π}{2}$)的部分图象如图所示,则f(x)的解析式为( )
已知函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,丨φ丨<$\frac{π}{2}$)的部分图象如图所示,则f(x)的解析式为( )| A. | f(x)=2sin(x+$\frac{π}{3}$) | B. | f(x)=2sin(2x+$\frac{π}{6}$) | C. | f(x)=2sin(2x-$\frac{π}{6}$) | D. | f(x)=2sin(4x-$\frac{π}{6}$) |
5.已知sinθ+cosθ=$\frac{2\sqrt{10}}{5}$,则tan(θ+$\frac{π}{4}$)=( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | ±$\frac{1}{2}$ | D. | ±2 |
12.命题p:函数y=log2($\sqrt{{x}^{2}+1}-x$)是奇函数,命题q:“对函数f(x),若f′(x0)=0,则x=x0为函数的极值点”.则下列命题中真命题是( )
| A. | p∧q | B. | p∨q | C. | (¬p)∧q | D. | (¬p)∧(¬q) |
6.在△ABC中,AC=5,BC=6,cos(A-B)=$\frac{37}{40}$,则△ABC面积是( )
| A. | 15 | B. | 10$\sqrt{2}$ | C. | 12 | D. | $\frac{3\sqrt{231}}{4}$ |
7.已知集合M={(x,y)|x2+y2≤1},若实数λ,μ满足:对任意的(x,y)∈M,都有(λx,μy)∈M,则称(λ,μ)是集合M的“和谐实数对”.则以下集合中,存在“和谐实数对”的是( )
| A. | {(λ,μ)|λ+μ=4} | B. | {(λ,μ)|λ2+μ2=4} | C. | {(λ,μ)|λ2-4μ=4} | D. | {(λ,μ)|λ2-μ2=4} |