题目内容
5.已知sinθ+cosθ=$\frac{2\sqrt{10}}{5}$,则tan(θ+$\frac{π}{4}$)=( )| A. | $\frac{1}{2}$ | B. | 2 | C. | ±$\frac{1}{2}$ | D. | ±2 |
分析 由题意和sin2θ+cos2θ=1联立解得sinθ和cosθ,进而可得tanθ,再由两角和的正切公式可得.
解答 解:∵sinθ+cosθ=$\frac{2\sqrt{10}}{5}$,sin2θ+cos2θ=1
联立解得$\left\{\begin{array}{l}{sinθ=\frac{3\sqrt{10}}{10}}\\{cosθ=\frac{\sqrt{10}}{10}}\end{array}\right.$或$\left\{\begin{array}{l}{sinθ=\frac{\sqrt{10}}{10}}\\{cosθ=\frac{3\sqrt{10}}{10}}\end{array}\right.$,
当$\left\{\begin{array}{l}{sinθ=\frac{3\sqrt{10}}{10}}\\{cosθ=\frac{\sqrt{10}}{10}}\end{array}\right.$时,tanθ=$\frac{sinθ}{cosθ}$=3,tan(θ+$\frac{π}{4}$)=$\frac{1+tanθ}{1-tanθ}$=-2;
当$\left\{\begin{array}{l}{sinθ=\frac{\sqrt{10}}{10}}\\{cosθ=\frac{3\sqrt{10}}{10}}\end{array}\right.$时,tanθ=$\frac{sinθ}{cosθ}$=$\frac{1}{3}$,tan(θ+$\frac{π}{4}$)=$\frac{1+tanθ}{1-tanθ}$=2.
故选:D
点评 本题考查两角和与差的三角函数公式,涉及同角三角函数基本关系和分类讨论的思想,属中档题.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
16.已知U=R,函数y=ln(1-x)的定义域为M,集合N={x|x2-x<0}.则下列结论正确的是( )
| A. | M∩N=N | B. | M∩(∁UN)=∅ | C. | M∪N=U | D. | M⊆(∁UN) |
20.若复数z满足zi=-1-i,则在复平面内,z所对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
10.函数f(x)=sin(2x+φ)(0<φ<π),若将函数y=f(x)的图象向左平移$\frac{π}{6}$个单位后所得图象对应的函数为偶函数,则实数φ的值为( )
| A. | $\frac{2π}{3}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
17.已知点A(0,4),B(-2,0),则线段AB中点C的坐标是( )
| A. | (-2,4) | B. | (-1,2) | C. | (1,2) | D. | (2,4) |
15.不等式($\frac{1}{2}$)${\;}^{2{x}^{2}+5x-5}$>2${\;}^{7-8x-{x}^{2}}$的解是( )
| A. | (1,2) | B. | (-∞,1)∪(2,+∞) | C. | (-2,-1) | D. | (-∞,-2)∪(-1,+∞) |
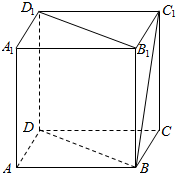 如图,正方体ABCD-A1B1C1D1中,直线BC1和B1D1所成角的大小为60°;直线BC1和平面B1D1DB所成角的大小为30°.
如图,正方体ABCD-A1B1C1D1中,直线BC1和B1D1所成角的大小为60°;直线BC1和平面B1D1DB所成角的大小为30°.