题目内容
19.已知数列{an}中,若a1=$\frac{1}{2}$,an=$\frac{1}{1-{a}_{n-1}}$(n≥2,n∈N+),则a2017等于( )| A. | 1 | B. | -1 | C. | $\frac{1}{2}$ | D. | 2 |
分析 利用数列递推关系可得an+3=an,再利用周期性即可得出.
解答 解:∵a1=$\frac{1}{2}$,an=$\frac{1}{1-{a}_{n-1}}$(n≥2,n∈N+),∴a2=$\frac{1}{1-\frac{1}{2}}$=2,同理可得:a3=-1,a4=$\frac{1}{2}$,…,
则an+3=an,
则a2017=a3×605+1=a1=$\frac{1}{2}$,
故选:C.
点评 本题考查了数列递推关系、数列的周期性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
14.已知S=(x-a)2+(lnx-a)2(a∈R),则S的最小值为( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{1}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
11.已知函数f(x)=$\left\{\begin{array}{l}{-lo{g}_{2}x,x≥0}\\{sin(πx+\frac{π}{6}),x<0}\end{array}\right.$,则f[f(8)]=( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
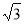 sin 2x,
sin 2x,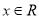
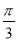 个单位后得到函数g(x)的图象,求函数g(x)的解析式,并求g(x)在[0,π]上的值域.
个单位后得到函数g(x)的图象,求函数g(x)的解析式,并求g(x)在[0,π]上的值域. 满足不等式
满足不等式 ,求函数
,求函数 (
( )的最小值
)的最小值 .
.