题目内容
8.已知函数f(x)=|lnx|,g(x)=$\left\{\begin{array}{l}{0,0<x≤1}\\{{|x}^{2}-1|-2,x>1}\end{array}\right.$,则方程|f(x)-g(x)=2的实根个数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 在同一个坐标系在画出两个函数的图象,观察有
解答 解:设F(x)=f(x)-2,F(x)与g(x)在同一个坐标系在的图象如图: 观察得到两个函数图象交点个数是1个,所以f(x)-g(x)=2的实根个数为1;
观察得到两个函数图象交点个数是1个,所以f(x)-g(x)=2的实根个数为1;
故选:A.
点评 本题考查了利用数形结合求方程根的个数问题;关键是正确将方程根的问题转化为函数图象的交点问题.

练习册系列答案
相关题目
19.已知数列{an}中,若a1=$\frac{1}{2}$,an=$\frac{1}{1-{a}_{n-1}}$(n≥2,n∈N+),则a2017等于( )
| A. | 1 | B. | -1 | C. | $\frac{1}{2}$ | D. | 2 |
3.设等差数列{an}的前n项和为Sn,公差为d,已知(a5-1)2015+2016a5+(a5-1)2017=2008,(a11-1)2015+2016a11+(a11-1)2017=2024,则下列命题是真命题的是( )
| A. | S15=22,d<0 | B. | S15=22,d>0 | C. | S15=15,d<0 | D. | S15=15,d>0 |
13.下列集合表示正确的是( )
| A. | {2,4} | B. | {2,4,4} | C. | (1,2,3) | D. | {高个子男生} |
 =2.347x-6.423;②y与x负相关且
=2.347x-6.423;②y与x负相关且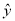 =-3.476x+5.648;③y与x正相关且
=-3.476x+5.648;③y与x正相关且