题目内容
11.已知函数f(x)=$\left\{\begin{array}{l}{-lo{g}_{2}x,x≥0}\\{sin(πx+\frac{π}{6}),x<0}\end{array}\right.$,则f[f(8)]=( )| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
分析 先求出f(8)=-log28=-3,从而f[f(8)]=f(-3)=sin(-3$π+\frac{π}{6}$),再利用正弦函数的诱导公式求解.
解答 解:∵函数f(x)=$\left\{\begin{array}{l}{-lo{g}_{2}x,x≥0}\\{sin(πx+\frac{π}{6}),x<0}\end{array}\right.$,
∴f(8)=-log28=-3,
f[f(8)]=f(-3)=sin(-3$π+\frac{π}{6}$)=-sin$\frac{π}{6}$=-$\frac{1}{2}$.
故选:A.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.设f(x)=sinx+cosx,若f′(x0)=$\sqrt{2}$,x0∈[-$\frac{π}{2}$,$\frac{π}{2}$],则函数在点(x0,f(x0))处的切线方程为( )
| A. | y=$\sqrt{2}$x+$\frac{\sqrt{2}π}{4}$ | B. | y=$\sqrt{2}$x-$\frac{\sqrt{2}π}{4}$ | C. | y=$\sqrt{2}$x-$\frac{\sqrt{2}π}{4}$+$\sqrt{2}$ | D. | y=$\sqrt{2}$x+$\frac{\sqrt{2}π}{4}$+$\sqrt{2}$ |
19.已知数列{an}中,若a1=$\frac{1}{2}$,an=$\frac{1}{1-{a}_{n-1}}$(n≥2,n∈N+),则a2017等于( )
| A. | 1 | B. | -1 | C. | $\frac{1}{2}$ | D. | 2 |
3.设等差数列{an}的前n项和为Sn,公差为d,已知(a5-1)2015+2016a5+(a5-1)2017=2008,(a11-1)2015+2016a11+(a11-1)2017=2024,则下列命题是真命题的是( )
| A. | S15=22,d<0 | B. | S15=22,d>0 | C. | S15=15,d<0 | D. | S15=15,d>0 |
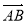 同方向的单位向量为( )
同方向的单位向量为( )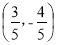 B.
B.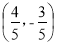
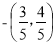 D.
D.