题目内容
7.已知数列满足a1=1,an=an-1+$\frac{1}{n(n-1)}$(n≥2),写出该数列的前5项及它的一个通项公式.分析 a1=1,an=an-1+$\frac{1}{n(n-1)}$(n≥2),可得a2=a1+$\frac{1}{2}$=$\frac{3}{2}$,同理可得:a3,a4,a5.由an=an-1+$\frac{1}{n(n-1)}$,可得an-an-1=$\frac{1}{n-1}-\frac{1}{n}$,利用“裂项求和”方法即可得出.
解答 解:∵a1=1,an=an-1+$\frac{1}{n(n-1)}$(n≥2),∴a2=a1+$\frac{1}{2}$=$\frac{3}{2}$,同理可得:a3=$\frac{5}{3}$,a4=$\frac{7}{4}$,a5=$\frac{9}{5}$.
∵an=an-1+$\frac{1}{n(n-1)}$,∴an-an-1=$\frac{1}{n-1}-\frac{1}{n}$,
∴an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1=$(\frac{1}{n-1}-\frac{1}{n})$+$(\frac{1}{n-2}-\frac{1}{n-1})$+…+$(1-\frac{1}{2})$+1=1-$\frac{1}{n}$+1=2-$\frac{1}{n}$,
点评 本题考查了数列递推关系、“裂项求和”方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
2.设f(x)=sinx+cosx,若f′(x0)=$\sqrt{2}$,x0∈[-$\frac{π}{2}$,$\frac{π}{2}$],则函数在点(x0,f(x0))处的切线方程为( )
| A. | y=$\sqrt{2}$x+$\frac{\sqrt{2}π}{4}$ | B. | y=$\sqrt{2}$x-$\frac{\sqrt{2}π}{4}$ | C. | y=$\sqrt{2}$x-$\frac{\sqrt{2}π}{4}$+$\sqrt{2}$ | D. | y=$\sqrt{2}$x+$\frac{\sqrt{2}π}{4}$+$\sqrt{2}$ |
19.已知数列{an}中,若a1=$\frac{1}{2}$,an=$\frac{1}{1-{a}_{n-1}}$(n≥2,n∈N+),则a2017等于( )
| A. | 1 | B. | -1 | C. | $\frac{1}{2}$ | D. | 2 |
 =2.347x-6.423;②y与x负相关且
=2.347x-6.423;②y与x负相关且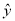 =-3.476x+5.648;③y与x正相关且
=-3.476x+5.648;③y与x正相关且 ;
; ,则
,则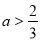 ;
;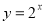 的图象与函数
的图象与函数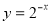 的图象关于y轴对称;
的图象关于y轴对称;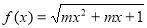 的定义域是R,则m的取值范围是
的定义域是R,则m的取值范围是 ;
;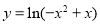 的递增区间为
的递增区间为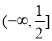 .
.