题目内容
4.在直角坐标系xoy中,圆C的参数方程为$\left\{\begin{array}{l}x=2+2cosφ\\ y=2sinφ\end{array}\right.$(φ为参数),以O为极点,x轴的非负半轴为极轴建立极坐标系.(1)求圆C的极坐标方程;
(2)若直线$l:\left\{\begin{array}{l}x=m+\frac{{\sqrt{3}}}{2}t\\ y=\frac{1}{2}t\end{array}\right.$(t为参数)与圆C交于A,B两点,且$|{AB}|=\sqrt{15}$,求m的值.
分析 (1)求出圆C的普通方程,可得圆C的极坐标方程;
(2)求出直线l的普通方程,利用勾股定理,建立方程,即可求出m的值.
解答 解:(1)圆C的参数方程为$\left\{\begin{array}{l}x=2+2cosφ\\ y=2sinφ\end{array}\right.$(φ为参数),普通方程为(x-2)2+y2=4,极坐标方程为ρ=4cosθ;
(2)直线$l:\left\{\begin{array}{l}x=m+\frac{{\sqrt{3}}}{2}t\\ y=\frac{1}{2}t\end{array}\right.$(t为参数),消去参数可得$\sqrt{3}$y-x+m=0,
圆心C到直线的距离d=$\frac{|m-2|}{2}$,
|AB|=2$\sqrt{4-\frac{(m-2)^{2}}{4}}$=$\sqrt{15}$,∴m=1或3.
点评 本题考查三种方程的转化,考查点到直线距离公式的运用,属于中档题.

练习册系列答案
相关题目
19.已知数列{an}中,若a1=$\frac{1}{2}$,an=$\frac{1}{1-{a}_{n-1}}$(n≥2,n∈N+),则a2017等于( )
| A. | 1 | B. | -1 | C. | $\frac{1}{2}$ | D. | 2 |
9.已知全集U={1,2,3},集合A={1},B={2},则∁U(A∪B)=( )
| A. | ∅ | B. | U | C. | {1,2} | D. | {3} |
13.下列集合表示正确的是( )
| A. | {2,4} | B. | {2,4,4} | C. | (1,2,3) | D. | {高个子男生} |
12.样本的数据如下:3,4,4,x,5,6,6,7,若该样本平均数为5,则样本方差为( )
| A. | 1.2 | B. | 1.3 | C. | 1.4 | D. | 1.5 |
 ;
; ,则
,则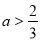 ;
;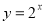 的图象与函数
的图象与函数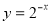 的图象关于y轴对称;
的图象关于y轴对称;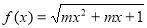 的定义域是R,则m的取值范围是
的定义域是R,则m的取值范围是 ;
;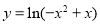 的递增区间为
的递增区间为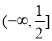 .
.