题目内容
14.已知S=(x-a)2+(lnx-a)2(a∈R),则S的最小值为( )| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{1}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
分析 由题意可得S的几何意义为两点(x.lnx),(a,a)的距离的平方,求得与直线y=x平行且与曲线y=lnx相切的切点的坐标,运用点到直线的距离公式计算即可得到所求最小值.
解答 解:S=(x-a)2+(lnx-a)2(a∈R)的几何意义为:
两点(x.lnx),(a,a)的距离的平方,
由y=lnx的导数为y′=$\frac{1}{x}$,
点(a,a)在直线y=x上,
令$\frac{1}{x}$=1,可得x=1,
即有与直线y=x平行的直线且与曲线y=lnx相切的切点为(1,0),
由点到直线的距离可得d=$\frac{|1-0|}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$,
即有S的最小值为($\frac{\sqrt{2}}{2}$)2=$\frac{1}{2}$,
故选:B.
点评 本题考查最值的求法,注意运用两点的距离的几何意义,考查导数的运用:求切线的斜率,以及点到直线的距离公式,考查转化能力和运算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.设f(x)=sinx+cosx,若f′(x0)=$\sqrt{2}$,x0∈[-$\frac{π}{2}$,$\frac{π}{2}$],则函数在点(x0,f(x0))处的切线方程为( )
| A. | y=$\sqrt{2}$x+$\frac{\sqrt{2}π}{4}$ | B. | y=$\sqrt{2}$x-$\frac{\sqrt{2}π}{4}$ | C. | y=$\sqrt{2}$x-$\frac{\sqrt{2}π}{4}$+$\sqrt{2}$ | D. | y=$\sqrt{2}$x+$\frac{\sqrt{2}π}{4}$+$\sqrt{2}$ |
9.设A、B分别为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右顶点,P,Q是双曲线C上关于x轴对称的不同两点,设直线AP、BQ的斜率分别为m、n,则$\frac{2b}{a}$+$\frac{a}{b}$+$\frac{1}{2|mn|}$+ln|m|+ln|n|取得最小值时,双曲线C的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{6}$ | D. | $\frac{\sqrt{6}}{2}$ |
19.已知数列{an}中,若a1=$\frac{1}{2}$,an=$\frac{1}{1-{a}_{n-1}}$(n≥2,n∈N+),则a2017等于( )
| A. | 1 | B. | -1 | C. | $\frac{1}{2}$ | D. | 2 |
3.设等差数列{an}的前n项和为Sn,公差为d,已知(a5-1)2015+2016a5+(a5-1)2017=2008,(a11-1)2015+2016a11+(a11-1)2017=2024,则下列命题是真命题的是( )
| A. | S15=22,d<0 | B. | S15=22,d>0 | C. | S15=15,d<0 | D. | S15=15,d>0 |
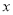 人,瓦工
人,瓦工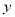 人,则工人满足的关系式是( )
人,则工人满足的关系式是( )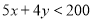 B.
B.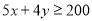
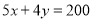 D.
D.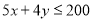
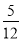 B.
B.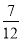 C.
C. D.
D.