题目内容
1.已知集合M={x|-1<x<3},N={x|x2-6x+8<0},则M∩N=( )| A. | (1,3) | B. | (2,3) | C. | (2,4) | D. | (1,4) |
分析 求出集合N的等价条件,结合集合的基本运算进行求解即可.
解答 解:N={x|x2-6x+8<0}={x|2<x<4},
则M∩N={x|2<x<3}=(2,3),
故选:B
点评 本题主要考查集合的基本运算,求出集合的等价条件是解决本题的关键.

练习册系列答案
相关题目
13.已知抛物线关于y轴对称,顶点在原点,且过点M(x0,3),点M到焦点的距离为4,则OM(O为坐标原点)等于( )
| A. | 2$\sqrt{3}$ | B. | $\sqrt{21}$ | C. | $\frac{\sqrt{45}}{2}$ | D. | 21 |
11.共享单车的出现方便了人们的出行,深受市民的喜爱.为调查某大学生对共享单车的使用情况,从该校学生中随机抽取了部分同学进行调查,得到男生、女生每周使用共享单车的时间(单位:小时)如下表:
按每周使用时间分层抽样的方法在这些学生中抽取10人,其中每周使用时间在[0,2]内的学生有2人.
(Ⅰ)求z的值;
(Ⅱ)将每周使用时间在(2,4]内的学生按性别分层抽样的方法抽取一个容量为6的样本.若从该样本中任取2人,求至少有1位女生的概率.
| 使用时间 | [0,2] | (2,4] | (4,6] |
| 女生人数 | 20 | 20 | z |
| 男生人数 | 20 | 40 | 60 |
(Ⅰ)求z的值;
(Ⅱ)将每周使用时间在(2,4]内的学生按性别分层抽样的方法抽取一个容量为6的样本.若从该样本中任取2人,求至少有1位女生的概率.
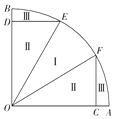 现有一个以OA、OB为半径的扇形池塘,在OA、OB上分别取点C、D,作DE∥OA、CF∥OB分别交弧AB于点E、F,且BD=AC,现用渔网沿着DE、EO、OF、FC将池塘分成如图所示的养殖区域.已知OA=1km,∠AOB=$\frac{π}{2}$,∠EOF=θ(0<θ<$\frac{π}{2}$).
现有一个以OA、OB为半径的扇形池塘,在OA、OB上分别取点C、D,作DE∥OA、CF∥OB分别交弧AB于点E、F,且BD=AC,现用渔网沿着DE、EO、OF、FC将池塘分成如图所示的养殖区域.已知OA=1km,∠AOB=$\frac{π}{2}$,∠EOF=θ(0<θ<$\frac{π}{2}$).