Question

10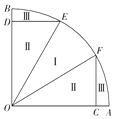．现有一个以OA、OB为半径的扇形池塘，在OA、OB上分别取点C、D，作DE∥OA、CF∥OB分别交弧AB于点E、F，且BD=AC，现用渔网沿着DE、EO、OF、FC将池塘分成如图所示的养殖区域．已知OA=1km，∠AOB=$\frac{π}{2}$，∠EOF=θ（0＜θ＜$\frac{π}{2}$）．
（1）若区域Ⅱ的总面积为$\frac{1}{4}k{m^2}$，求θ的值；
（2）若养殖区域Ⅰ、Ⅱ、Ⅲ的每平方千米的年收入分别是30万元、40万元、20万元，试问：当θ为多少时，年总收入最大？

Answer 1

分析 （1）推导出OD=OC，DE⊥OB，CF⊥OA，从而Rt△ODE≌Rt△OCF，进而∠DOE=∠COF=$\frac{1}{2}（{\frac{π}{2}-θ}）$，由此得到S_区域Ⅱ=$\frac{1}{2}cosθ$（0＜θ＜$\frac{π}{2}$），从而能求出θ．
（2）由S_区域Ⅰ=$\frac{1}{2}θ$，求出S_区域Ⅲ=S_总-S_区域Ⅰ-S_区域Ⅱ=$\frac{π}{4}-\frac{1}{2}θ-\frac{1}{2}$cosθ．记年总收入为y万元，则y=5π+5θ+10cosθ（0＜θ＜$\frac{π}{2}$），y'=5（1-2sinθ），令y'=0，则θ=$\frac{π}{6}$．由此利用导数性质求出当θ=$\frac{π}{6}$时，年总收入最大．

解答 解：（1）∵BD=AC，OB=OA，∴OD=OC．
∵∠AOB=$\frac{π}{2}$，DE∥OA，CF∥OB，
∴DE⊥OB，CF⊥OA．
又∵OE=OF，∴Rt△ODE≌Rt△OCF．
∴∠DOE=∠COF=$\frac{1}{2}（{\frac{π}{2}-θ}）$，
又OC=OF•cos∠COF
∴S_△COF=$\frac{1}{2}$•OC•OF•sin∠COF=$\frac{1}{4}$cosθ
∴S_区域Ⅱ=$\frac{1}{2}cosθ$（0＜θ＜$\frac{π}{2}$）．
由$\frac{1}{2}cosθ=\frac{1}{4}$，得cosθ=$\frac{1}{2}$，
∵0＜θ＜$\frac{π}{2}$，∴θ=$\frac{π}{3}$．
（2）∵S_区域Ⅰ=$\frac{1}{2}θ$，∴S_区域Ⅲ=S_总-S_区域Ⅰ-S_区域Ⅱ=$\frac{π}{4}-\frac{1}{2}θ-\frac{1}{2}$cosθ．
记年总收入为y万元，
则y=30×$\frac{1}{2}θ+40×\frac{1}{2}$cosθ$+20×（{\frac{π}{4}-\frac{1}{2}θ}$$\left.{-\frac{1}{2}cosθ}）$=5π+5θ+10cosθ（0＜θ＜$\frac{π}{2}$），
所以y'=5（1-2sinθ），令y'=0，则θ=$\frac{π}{6}$．
当0＜θ＜$\frac{π}{6}$时，y'＞0；当$\frac{π}{6}＜θ＜\frac{π}{2}$时，y'＜0．
故当θ=$\frac{π}{6}$时，y有最大值，即年总收入最大．

点评 本题考查扇形面积、导数的性质及应用、函数性质、构造法等基础知识，考查推理论证能力、运算求解能力，考查化归与转化思想、函数与方程思想，是中档题．