题目内容
解下列各一元二次不等式:
(1)2x2-4x+2>0;
(2)-x2+3x+10≥0.
(1)2x2-4x+2>0;
(2)-x2+3x+10≥0.
考点:一元二次不等式的解法
专题:不等式的解法及应用
分析:根据一元二次不等式的特征,选择适当的解法与步骤,进行解答即可.
解答:
解:(1)不等式2x2-4x+2>0可化为
x2-2x+1>0,
即(x-1)2>0,
解得x≠1,
∴不等式是解集为{x|x≠1};
(2)不等式-x2+3x+10≥0可化为
x2-3x-10≤0,
即(x-5)(x+2)≤0;
解得-2≤x≤5,
∴不等式的解集为[-2,5].
x2-2x+1>0,
即(x-1)2>0,
解得x≠1,
∴不等式是解集为{x|x≠1};
(2)不等式-x2+3x+10≥0可化为
x2-3x-10≤0,
即(x-5)(x+2)≤0;
解得-2≤x≤5,
∴不等式的解集为[-2,5].
点评:本题考查了一元二次不等式的解法与应用问题,是基础题目.

练习册系列答案
相关题目
已知函数f(x)=xα,α∈{-1,
,1,2,3},若f(x)是区间(-∞,+∞)上的增函数,则α的所有可能取值为( )
| 1 |
| 2 |
| A、{1,3} | ||
B、{
| ||
| C、{1,2,3} | ||
D、{-1,
|
函数f(x)=[x]的函数值表示不超过x的最大整数,例如,[-3.5]=-4,[2.1]=2.当x∈(-2.5,3]时,函数f(x)的值域为( )
| A、{-2,-1,0,1,2} |
| B、{-3,-2,-1,0,1,2} |
| C、{-2,-1,0,1,2,3} |
| D、{-3,-2,-1,0,1,2,3} |
已知△ABC的内角A,B,C对应的边分别为a,b,c,且
=
,则△ABC为( )
| c |
| a |
| cosB |
| 1+cosA |
| A、等边三角形 |
| B、等腰直角三角形 |
| C、直角三角形 |
| D、三边均不相等的三角形 |
为了得到函数f(x)=2sin(2x-
)的图象,只要将y=2sinx的图象上所有的点( )
| π |
| 3 |
A、向右平移
| ||||
B、向右平移
| ||||
C、向右平移
| ||||
D、向右平移
|
设全集为实数集R,M={x|x2>4},N={x|1<x≤3},则图中阴影部分表示的集合是( ) 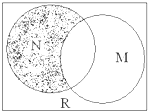

| A、{x|1-2≤x<1} |
| B、{x|-2≤x≤2} |
| C、{x|1<x≤2} |
| D、{x|x<2} |