Question

8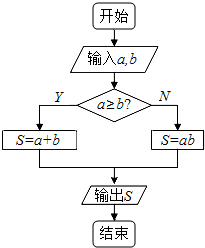．定义一种运算S=a?b，在如图所示的框图所表达的算法中揭示了这种运算“?”的含义，那么按照运算“?”的含义，S=tan60°?tan30°+cos60°?cos30°=（　　）

• A． $\frac{{3+\sqrt{3}}}{2}$
• B． $\frac{{4+\sqrt{3}}}{4}$
• C． $\frac{{19\sqrt{3}}}{12}$
• D． $\frac{{11\sqrt{3}}}{6}+\frac{1}{2}$

Answer 1

分析 先利用特殊角的三角函数值比较大小，然后根据题中选择结构将所求式子的新定义运算转化为普通运算，即可求值．

解答 解：∵tan60°=$\sqrt{3}＞$tan30°=$\frac{\sqrt{3}}{3}$，cos60°=$\frac{1}{2}$＜cos30°=$\frac{\sqrt{3}}{2}$，
∴S=tan60°?tan30°+cos60°?cos30°=$tan60°+tan30°+cos60°×cos30°=\frac{{19\sqrt{3}}}{12}$．
故选：C．

点评 此题考查了特殊角的三角函数值，属于新定义的题型，理解本题的选择结构是解本题的关键，属于基础题．