题目内容
17.求下列曲线的标准方程:(1)与椭圆x2+4y2=16有相同焦点,过点$P(\sqrt{5},\sqrt{6})$;
(2)与椭圆$\frac{x^2}{8}$+$\frac{y^2}{4}$=1有相同的焦点,直线y=$\sqrt{3}$x为一条渐近线,求双曲线C的方程.
(3)焦点在直线3x-4y-12=0的抛物线的标准方程.
分析 (1)(2)利用待定系数法求方程;
(3)先根据抛物线是标准方程可确定焦点的位置,再由直线3x-4y-12=0与坐标轴的交点可得到焦点坐标,根据抛物线的焦点坐标和抛物线的标准形式可得到标准方程.
解答 解:(1)椭圆x2+4y2=16,可化为$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{4}$=1,焦点(±2$\sqrt{3}$,0)
设椭圆的方程为$\frac{{x}^{2}}{16+m}+\frac{{y}^{2}}{4+m}$=1,
代入$P(\sqrt{5},\sqrt{6})$,可得$\frac{5}{16+m}+\frac{6}{4+m}$=1,
∴m=4,
∴椭圆的方程为$\frac{x^2}{20}+\frac{y^2}{8}=1$
(2)椭圆$\frac{x^2}{8}$+$\frac{y^2}{4}$=1的焦点为(±2,0),∴c=2,
∵直线y=$\sqrt{3}$x为一条渐近线,
∴$\frac{b}{a}$=$\sqrt{3}$,
∴a=1,b=$\sqrt{3}$,
∴双曲线C的方程为$\frac{x^2}{1}-\frac{y^2}{3}=1$;
(3)因为是标准方程,所以其焦点应该在坐标轴上,
所以其焦点坐标即为直线3x-4y-12=0与坐标轴的交点
所以其焦点坐标为(4,0)和(0,-3)
当焦点为(4,0)时可知其方程中的P=8,所以其方程为y2=16x,
当焦点为(0,-3)时可知其方程中的P=6,所以其方程为x2=-12y,
综上所述,抛物线的方程为y2=16x或x2=-12y.
点评 本题考查曲线方程,考查待定系数法的运用,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
8.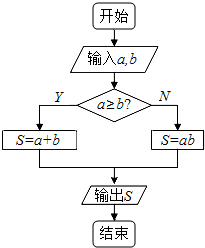 定义一种运算S=a?b,在如图所示的框图所表达的算法中揭示了这种运算“?”的含义,那么按照运算“?”的含义,S=tan60°?tan30°+cos60°?cos30°=( )
定义一种运算S=a?b,在如图所示的框图所表达的算法中揭示了这种运算“?”的含义,那么按照运算“?”的含义,S=tan60°?tan30°+cos60°?cos30°=( )
 定义一种运算S=a?b,在如图所示的框图所表达的算法中揭示了这种运算“?”的含义,那么按照运算“?”的含义,S=tan60°?tan30°+cos60°?cos30°=( )
定义一种运算S=a?b,在如图所示的框图所表达的算法中揭示了这种运算“?”的含义,那么按照运算“?”的含义,S=tan60°?tan30°+cos60°?cos30°=( )| A. | $\frac{{3+\sqrt{3}}}{2}$ | B. | $\frac{{4+\sqrt{3}}}{4}$ | C. | $\frac{{19\sqrt{3}}}{12}$ | D. | $\frac{{11\sqrt{3}}}{6}+\frac{1}{2}$ |
5.已知一个正方体的所有棱与空间的某一平面成角为α,则cosα的值为( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{6}}{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{6}$ |
12.正项等比数列{an}中,a1a3+2a2a3+a1a5=16,则a2+a3的值为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
2.函数f(x)=2sin(ωx+φ)(ω>0,一$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则( )
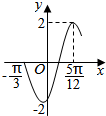
| A. | 函数f(x)的最小正周期是2π | |
| B. | 函数f(x)的图象可由函数g(x)=2sin2x的图象向右平移$\frac{π}{3}$个单位长度得到 | |
| C. | 函数f(x)的图象关于直线x=一$\frac{π}{12}$对称 | |
| D. | 函数f(x)在区间[-$\frac{7π}{12}$+kπ,-$\frac{π}{12}$+kπ](k∈Z)上是增函数 |
9.设点O(0,0,0),A(2,-1,3),B(-1,4,-2),C(3,1,λ),若O,A,B,C四点共面,则实数λ等于( )
| A. | $\frac{26}{7}$ | B. | $\frac{27}{7}$ | C. | 4 | D. | $\frac{29}{7}$ |
6.阅读如图所示的程序框图,输出的结果为( )


| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
7.函数f(x)=6-x-x2的单调递减区间是( )
| A. | $[-\frac{1}{2},+∞)$ | B. | $[-\frac{1}{2},2)$ | C. | $(-∞,-\frac{1}{2}]$ | D. | (-3,$-\frac{1}{2}]$ |