题目内容
20．在等差数列{an}中，a20l5=a2013+6，则公差d等于（ ）| A． | 2 | B． | 3 | C． | 4 | D． | 6 |
分析 在等差数列中，直接利用$d=\frac{{a}_{n}-{a}_{m}}{n-m}$求得公差．
解答 解：在等差数列{an}中，由a20l5=a2013+6，
得2d=a20l5-a2013=6，即d=3．
故选：B．
点评 本题考查等差数列的通项公式，是基础的计算题．
练习册系列答案
阳光课堂课时作业系列答案
相关题目
8．
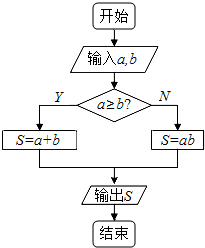定义一种运算S=a?b，在如图所示的框图所表达的算法中揭示了这种运算“?”的含义，那么按照运算“?”的含义，S=tan60°?tan30°+cos60°?cos30°=（ ）
定义一种运算S=a?b，在如图所示的框图所表达的算法中揭示了这种运算“?”的含义，那么按照运算“?”的含义，S=tan60°?tan30°+cos60°?cos30°=（ ）| A． | $\frac{{3+\sqrt{3}}}{2}$ | B． | $\frac{{4+\sqrt{3}}}{4}$ | C． | $\frac{{19\sqrt{3}}}{12}$ | D． | $\frac{{11\sqrt{3}}}{6}+\frac{1}{2}$ |
5．已知一个正方体的所有棱与空间的某一平面成角为α，则cosα的值为（ ）
| A． | $\frac{\sqrt{3}}{3}$ | B． | $\frac{\sqrt{6}}{3}$ | C． | $\frac{\sqrt{2}}{2}$ | D． | $\frac{\sqrt{3}}{6}$ |
12．正项等比数列{an}中，a1a3+2a2a3+a1a5=16，则a2+a3的值为（ ）
| A． | 3 | B． | 4 | C． | 5 | D． | 6 |
9．设点O（0，0，0），A（2，-1，3），B（-1，4，-2），C（3，1，λ），若O，A，B，C四点共面，则实数λ等于（ ）
| A． | $\frac{26}{7}$ | B． | $\frac{27}{7}$ | C． | 4 | D． | $\frac{29}{7}$ |