题目内容
9.若x>0,y>0,且$\frac{1}{x}+\frac{1}{y}=\frac{1}{2}$,则xy有( )| A. | 最大值16 | B. | 最小值$\frac{1}{16}$ | C. | 最小值16 | D. | 最小值$\frac{1}{2}$ |
分析 由已知可得$\frac{1}{x}、\frac{1}{y}$均为正数,然后结合基本不等式可得xy有最小值.
解答 解:由$\frac{1}{x}+\frac{1}{y}=\frac{1}{2}$,且x>0,y>0,
得$\frac{1}{2}=\frac{1}{x}+\frac{1}{y}≥2\sqrt{\frac{1}{xy}}$,∴$\sqrt{\frac{1}{xy}}≤\frac{1}{4}$,则xy≥16(当且仅当x=y=4时等号成立).
∴xy有最小值16.
故选:C.
点评 本题考查简单的线性规划,训练了利用基本不等式求最值,是中档题.

练习册系列答案
相关题目
20.下列各组函数表示相等函数的是( )
| A. | $f(x)={({\sqrt{x}})^2}$和$g(x)=\sqrt{x^2}$ | B. | $f(x)={({\root{3}{x+1}})^3}$和$g(x)=\root{3}{{{{({x+1})}^3}}}$ | ||
| C. | f(x)=2lgx和g(x)=lg x2 | D. | f(x)=ln x-ln(x-1)和$g(x)=ln\frac{x}{x-1}$ |
4.“$\left\{{x\left|{\frac{1}{x}≤1}\right.}\right\}$”是“{x|lnx≥0}”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
18.设△ABC的内角A,B,C所对的边分别为a,b,c若cos2$\frac{B}{2}=\frac{a+c}{2c}$,则△ABC的形状为( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 不确定 |
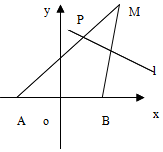 已知A点坐标为$(-2\sqrt{3},0)$,B点坐标为$(2\sqrt{3},0)$,且动点M到A点的距离是8,线段MB的垂直平分线l交线段MA于点P.
已知A点坐标为$(-2\sqrt{3},0)$,B点坐标为$(2\sqrt{3},0)$,且动点M到A点的距离是8,线段MB的垂直平分线l交线段MA于点P.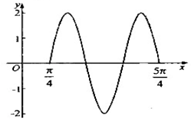 已知函数f(x)=2sin(ωx+φ),(ω>0,0≤φ<2π)的部分图象如图所示,则f(x)=2sin(3x+$\frac{5π}{4}$).
已知函数f(x)=2sin(ωx+φ),(ω>0,0≤φ<2π)的部分图象如图所示,则f(x)=2sin(3x+$\frac{5π}{4}$).