题目内容
10.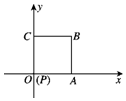 如图放置的边长为2的正方形PABC沿x轴正半轴滚动.设顶点P(x,y)的轨迹方程是y=f(x),则f(x)的最小正周期为8;y=f(x)在其两个相邻零点间的图象与x轴所围区域的面积为4π+4.
如图放置的边长为2的正方形PABC沿x轴正半轴滚动.设顶点P(x,y)的轨迹方程是y=f(x),则f(x)的最小正周期为8;y=f(x)在其两个相邻零点间的图象与x轴所围区域的面积为4π+4.
分析 P点的运动轨迹为若干个$\frac{1}{4}$圆周拼接而成,作出P点轨迹图象,即可得出答案.
解答 解:P点从x轴上开始运动的时候,首先是围绕A点运动$\frac{1}{4}$个圆,该圆半径为2,
然后以B点为中心,滚动到C点落地,其间是以BP为半径,旋转90°,
再以C为圆心,再旋转90°,这时候以CP为半径,因此最终构成图象如下: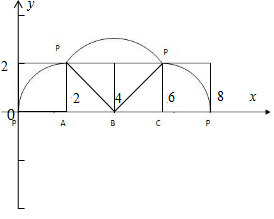
由轨迹可知f(x)的最小正周期为8,
S=2×$\frac{1}{4}$π•22+2×$\frac{1}{2}$×2×2+$\frac{1}{4}$×π•(2$\sqrt{2}$)2=4π+4.
故答案为:8;4π+4.
点评 本题考查的知识点是函数图象的变化,其中根据已知画出正方形转动过程中的一个周期内的图象,利用数形结合的思想对本题进行分析是解答本题的关键.

练习册系列答案
相关题目
20.下列各组函数表示相等函数的是( )
| A. | $f(x)={({\sqrt{x}})^2}$和$g(x)=\sqrt{x^2}$ | B. | $f(x)={({\root{3}{x+1}})^3}$和$g(x)=\root{3}{{{{({x+1})}^3}}}$ | ||
| C. | f(x)=2lgx和g(x)=lg x2 | D. | f(x)=ln x-ln(x-1)和$g(x)=ln\frac{x}{x-1}$ |
18.设△ABC的内角A,B,C所对的边分别为a,b,c若cos2$\frac{B}{2}=\frac{a+c}{2c}$,则△ABC的形状为( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 不确定 |
2.设{an}是首项为a1,公差为-1的等差数列,sn为其前n项和,s2是s1与s4的等比中项,则a1=( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
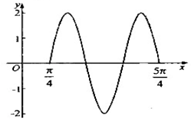 已知函数f(x)=2sin(ωx+φ),(ω>0,0≤φ<2π)的部分图象如图所示,则f(x)=2sin(3x+$\frac{5π}{4}$).
已知函数f(x)=2sin(ωx+φ),(ω>0,0≤φ<2π)的部分图象如图所示,则f(x)=2sin(3x+$\frac{5π}{4}$).