Question

某几何体的三视图及其尺寸如图所示，则该几何体的表面积是（　　）

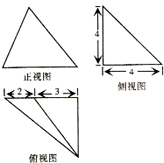
• A、30+6

  5

• B、28+6

  5

• C、56+12

  5

• D、60+12

  5

Answer 1

考点：棱柱、棱锥、棱台的体积,由三视图求面积、体积

专题：空间位置关系与距离

分析：画出几何体的直观图，判断图形的表面三角形的形状，然后求解表面积．

解答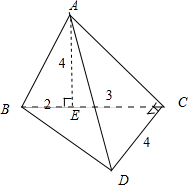： 解：三视图复原几何体如图：AE⊥平面BCD，BC⊥CD，∴DC⊥AC，
AE=4，BE=2，EC=3，CD=4，
∴AB=

42+22

=2

5

，BD=

52+42

=

41

，AC=5，
AD=

52+42

=

41

，
∴S△ABD=

1

2

AB•

BD2+( 1 2 AB)2

=

1

2

×2

5

×

41-5

=6

5

．
S△ABC=

1

2

BC•AE=

1

2

×5×4=10．
S△ADC=

1

2

DC•AC=

1

2

×5×4=10．
S△DBC=

1

2

BC•CD=

1

2

×5×4=10．
S_表=30+6

5

．
故选：A．

点评：本题考查了由三视图求几何体的表面积，根据三视图判断几何体的形状及数据所对应的几何量是解题的关键．