题目内容
设函数f(x)满足xf′(x)+f(x)=
,f(e)=
,则函数f(x)( )
| lnx |
| x |
| 1 |
| e |
| A、在(0,e)上单调递增,在(e,+∞)上单调递减 |
| B、在(0,+∞)上单调递增 |
| C、在(0,e)上单调递减,在(e,+∞)上单调递增 |
| D、在(0,+∞)上单调递减 |
考点:函数的单调性与导数的关系,导数的运算,利用导数研究函数的单调性
专题:导数的概念及应用
分析:首先求出函数f(x),再求导,判断函数的单调性
解答:
解:∵[x(f(x)]′=xf′(x)+f(x),
∴[xf(x)]′=
=(
+c)′
∴xf(x)=
ln2x+c
∴f(x)=
+
∵f(e)=
,
∴
=
+
即c=
∴f′(x)=
-
=-
=-
<0
∴f(x)在(0,+∞)为减函数.
故选:D.
∴[xf(x)]′=
| lnx |
| x |
| ln2x |
| 2 |
∴xf(x)=
| 1 |
| 2 |
∴f(x)=
| ln2x |
| 2x |
| c |
| x |
∵f(e)=
| 1 |
| e |
∴
| 1 |
| e |
| 1 |
| 2e |
| c |
| e |
即c=
| 1 |
| 2 |
∴f′(x)=
| 2lnx-ln2x |
| 2x2 |
| 1 |
| 2x2 |
| ln2x-2lnx+1 |
| 2x2 |
| (lnx-1)2 |
| 2x2 |
∴f(x)在(0,+∞)为减函数.
故选:D.
点评:本题主要考查了导数和函数的单调性的关系,关键是求出函数f(x),属于中档题.

练习册系列答案
相关题目
函数f(x)=sin(ωx+φ)(ω>0,|φ|<
)的最小正周期为π,且其图象向左平移
个单位后得到的函数为奇函数,则函数f(x)的图象( )
| π |
| 2 |
| π |
| 12 |
A、关于点(
| ||
B、关于直线x=
| ||
C、关于点(
| ||
D、关于直线x=
|
某几何体的三视图及其尺寸如图所示,则该几何体的表面积是( )
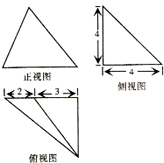

A、30+6
| ||
B、28+6
| ||
C、56+12
| ||
D、60+12
|
已知sinα>0,cosα>0,则角α的终边落在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
设ω∈(0,10],则函数y=sinωx在区间(-
,
)上是增函数的概率是( )
| π |
| 3 |
| π |
| 6 |
A、
| ||
B、
| ||
C、
| ||
D、
|
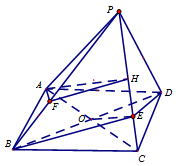 四棱锥P-ABCD中,底面ABCD是平行四边形,E∈PC,F∈PB,
四棱锥P-ABCD中,底面ABCD是平行四边形,E∈PC,F∈PB,