题目内容
9．函数$f（x）=\frac{2x-1}{e^x}$在x=1处的切线的斜率为$\frac{1}{e}$．分析 对函数$f（x）=\frac{2x-1}{e^x}$求导，当x=1时，求出f'（1）即可．
解答 解：对函数$f（x）=\frac{2x-1}{e^x}$求导：f'（x）=$\frac{3-2x}{{e}^{x}}$，
当x=1时，f'（1）=$\frac{1}{e}$．
故答案为$\frac{1}{e}$．
点评 本题主要考查利用导数求曲线的斜率，属基础题．
练习册系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
17．某几何体的三视图如图所示，则该几何体的表面积为（ ）
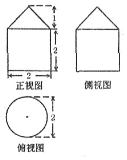
| A． | $\frac{7π}{3}$ | B． | $8+\frac{π}{3}$ | C． | $（{4+\sqrt{2}}）π$ | D． | $（{5+\sqrt{2}}）π$ |
4．若从2个海滨城市和2个内陆城市中随机选2个去旅游，那么恰好选1个海滨城市的概率是（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{2}{3}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{2}$ |
