题目内容
19.一个几何体,其三视图如图所示,则该几何体的体积为$\frac{\sqrt{2}}{6}π$+$\frac{1}{3}$.
分析 由三视图可知:该几何体由一个半球与一个正四棱锥组成的.
解答 解:由三视图可知:该几何体由一个半球与一个正四棱锥组成的.
该几何体的体积V=$\frac{1}{2}×\frac{4π}{3}×(\frac{\sqrt{2}}{2})^{3}$+$\frac{1}{3}×{1}^{2}×1$=$\frac{\sqrt{2}}{6}π$+$\frac{1}{3}$.
故答案为:$\frac{\sqrt{2}}{6}π$+$\frac{1}{3}$.
点评 本题考查了球与正四棱锥的三视图、体积计算公式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.已知p,q是简单命题,那么“p∧q是真命题”是“¬p是真命题”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
4.执行如图所示的程序框图,则输出的结果是( )


| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
15.全集U={1,2,3,4,5,6},若M={1,4},N={2,3},则∁U(M∪N)等于( )
| A. | {1,2,3,4} | B. | {3,4} | C. | {1,6} | D. | {5,6} |
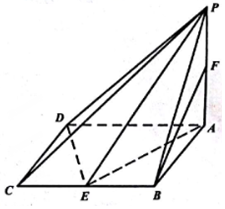 在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠BAD=60°,PA=$\sqrt{3}$,PA⊥面ABCD,E、F分别为BC、PA的中点.
在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠BAD=60°,PA=$\sqrt{3}$,PA⊥面ABCD,E、F分别为BC、PA的中点.