题目内容
如果直线a和直线b是异面直线，直线c∥a，那么直线b与c（ ）
| A、异面 | B、相交 |
| C、平行 | D、异面或相交 |
考点：空间中直线与直线之间的位置关系
专题：空间位置关系与距离
分析：直线b和c有可能在同一平面上，也有可能不在同一平面上，如果b和c在同一平面上的话，二者的位置关系为相交；如果b和c不在同一平面上，二者的位置关系为异面．
解答：
解：∵直线a与b是异面直线，直线c∥a，
∴直线b和c有可能在同一平面上，也有可能不在同一平面上，
如果b和c在同一平面上的话，二者的位置关系为相交；
如果b和c不在同一平面上，二者的位置关系为异面．
故选：D．
∴直线b和c有可能在同一平面上，也有可能不在同一平面上，
如果b和c在同一平面上的话，二者的位置关系为相交；
如果b和c不在同一平面上，二者的位置关系为异面．
故选：D．
点评：本题考查两条直线的位置关系的判断，是基础题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
举一反三单元同步过关卷系列答案
相关题目
已知三次函数f（x）=
x3-（4m-1）x2+（15m2-2m-7）x+2在x∈（-∞，+∞）是增函数，则m的取值范围是（ ）
| 1 |
| 3 |
| A、m＜2或m＞4 |
| B、2≤m≤4 |
| C、2＜m＜4 |
| D、-4＜m＜-2 |
在三棱柱ABC-A1B1C1中，已知AA1⊥平面ABC，AA1=2，BC=2
，∠BAC=
，此三棱柱各个顶点都在一个球面上，则球的体积为（ ）
| 3 |
| π |
| 2 |
A、
| ||
| B、16π | ||
C、
| ||
D、
|
在△ABC中，a=2，b=
，c=30°，则△ABC的面积是（ ）
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
随机变量Y满足P（Y=c）=1，其中c为常数，则D（Y）等于（ ）
| A、0 | B、c（1-c） | C、c | D、1 |
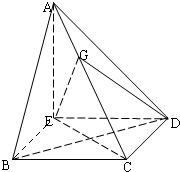如图，在四棱锥A-BCDE中，AE⊥平面BCDE，∠ABC=∠BCD=∠CDA=90°，AC=6