题目内容
已知α是第二象限的角,若cosα=m,则sin(3π+α)+
sin(2π-α)等于 .
| 1 |
| 2 |
考点:运用诱导公式化简求值
专题:集合
分析:由α为第二象限角,由cosα,利用同角三角函数间基本关系表示出sinα,原式利用诱导公式化简后将各自的值代入计算即可求出值.
解答:
解:∵α是第二象限的角,cosα=m,
∴sinα=
,
则原式=-sinα-
sinα=-
sinα=-
.
故答案为:-
∴sinα=
| 1-m2 |
则原式=-sinα-
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 1-m2 |
故答案为:-
| 3 |
| 2 |
| 1-m2 |
点评:此题考查了运用诱导公式化简求值,熟练掌握诱导公式是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若(x+
)n展开式中只有第6项的系数最大,则常数项是( )
| 1 |
| x |
| A、第5项 | B、第6项 |
| C、第7项 | D、第8项 |
高三年级的三个班去甲、乙、丙、丁四个工厂参加社会实践,但去何工厂可自由选择,甲工厂必须有班级要去,则不同的分配方案有( )
| A、16种 | B、18种 |
| C、37种 | D、48种 |
函数f(x)的定义域为R,其导函数f′(x)的图象如图所示,则函数f(x)( )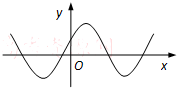

| A、有三个极值点,但无法判断有几个极大值,几个极小值 |
| B、有一个极大值点,两个极小值点 |
| C、有两个极大值点,两个极小值点 |
| D、有四个极值点,但无法判断有几个极大值,几个极小值 |
函数f(x)=cos(x2+x)导数是( )
| A、-sin(x2+x) |
| B、-(2x+1)sin(x2+x) |
| C、-2xsin(x2+x) |
| D、(2x+1)sin(x2+x) |
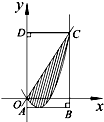 如图,矩形ABCD内的阴影部分是由曲线f(x)=2x2-2x及直线y=2x围成的,现向矩形ABCD内随机投掷一点,则该点落在阴影部分的概率为
如图,矩形ABCD内的阴影部分是由曲线f(x)=2x2-2x及直线y=2x围成的,现向矩形ABCD内随机投掷一点,则该点落在阴影部分的概率为