题目内容
15.已知函数f(x)=$\frac{1}{2}$ax2+lnx,其中a∈R.(1)求函数f(x)的单调区间;
(2)若a<-1,f(x)在(0,1]上的最大值为-1,求a的值.
分析 (1)f′(x)=ax+$\frac{1}{x}$=$\frac{a{x}^{2}+1}{x}$,(x>0).对a分类讨论:当a≥0时,f′(x)>0,即可得出f(x)在(0,+∞)上单调递增.当a<0时,f′(x)=$\frac{a(x+\sqrt{\frac{-1}{a}})(x-\sqrt{\frac{-1}{a}})}{x}$,进而得出单调性.
(2)a<-1时,$\sqrt{\frac{-1}{a}}$∈(0,1).由(1)可得:函数f(x)在(0,$\sqrt{\frac{-1}{a}}$)上单调递增,在($\sqrt{\frac{-1}{a}}$,1]上单调递减,可得当x=$\sqrt{\frac{-1}{a}}$时,函数f(x)取得极大值即最大值,利用$f(\sqrt{\frac{-1}{a}})$=-1,解出即可得出.
解答 解:(1)f′(x)=ax+$\frac{1}{x}$=$\frac{a{x}^{2}+1}{x}$,(x>0).
当a≥0时,f′(x)>0,此时函数f(x)在(0,+∞)上单调递增;
当a<0时,f′(x)=$\frac{a(x+\sqrt{\frac{-1}{a}})(x-\sqrt{\frac{-1}{a}})}{x}$,
则函数f(x)在($\sqrt{\frac{-1}{a}}$,+∞)上单调递减,在(0,$\sqrt{\frac{-1}{a}}$)上单调递增.
综上可得:当a≥0时,函数f(x)在(0,+∞)上单调递增.
当a<0时,函数f(x)在($\sqrt{\frac{-1}{a}}$,+∞)上单调递减,在(0,$\sqrt{\frac{-1}{a}}$)上单调递增.
(2)a<-1时,$\sqrt{\frac{-1}{a}}$∈(0,1).
由(1)可得:函数f(x)在(0,$\sqrt{\frac{-1}{a}}$)上单调递增,在($\sqrt{\frac{-1}{a}}$,1]上单调递减,
∴当x=$\sqrt{\frac{-1}{a}}$时,函数f(x)取得极大值即最大值,∴$f(\sqrt{\frac{-1}{a}})$=$\frac{1}{2}a×(-\frac{1}{a})$+ln$\sqrt{\frac{-1}{a}}$=-1,
∴ln$\sqrt{\frac{-1}{a}}$=-$\frac{1}{2}$,解得a=-e.
点评 本题考查了利用导数研究函数的单调性极值与最值、方程与不等式的解法,考查了分类讨论方法、推理能力与计算能力,属于难题.

| A. | [$\frac{ln3}{3}$,$\frac{1}{e}$) | B. | [ln3,$\frac{3}{e}$) | C. | [ln3,$\frac{1}{e}$) | D. | (0,$\frac{1}{e}$) |
| 文科 | 理科 | |
| 数学优秀 | 10 | 13 |
| 数学不优秀 | 20 | 7 |
 如图所示是y=f(x)的导数图象,则正确的判断是( )
如图所示是y=f(x)的导数图象,则正确的判断是( )①f(x)在(-3,1)上是增函数;
②x=-1是f(x)的极小值点;
③x=2是f(x)的极小值点;
④f(x)在(2,4)上是减函数,在(-1,2)上是增函数.
| A. | ①②④ | B. | ②④ | C. | ③④ | D. | ①③④ |
| A. | 8$\sqrt{5}$ | B. | 4$\sqrt{5}$ | C. | 12 | D. | 24 |
 如图,在平行四边形ABCD中,点E在AB上且EB=2AE,AC与DE交于点F,则△CDF的周长与△AEF的周长之比为( )
如图,在平行四边形ABCD中,点E在AB上且EB=2AE,AC与DE交于点F,则△CDF的周长与△AEF的周长之比为( )| A. | 1:3 | B. | 3:1 | C. | 1:2 | D. | 2:1 |
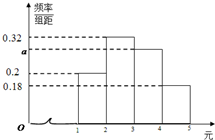 甲、乙、丙三人参加微信群抢红包游戏,规则如下:每轮游戏发50个红包,每个红包金额为x元,x∈[1,5].已知在每轮游戏中所产生的50个红包金额的频率分布直方图如图所示.
甲、乙、丙三人参加微信群抢红包游戏,规则如下:每轮游戏发50个红包,每个红包金额为x元,x∈[1,5].已知在每轮游戏中所产生的50个红包金额的频率分布直方图如图所示.