题目内容
4．函数f（x）=loga（2x-3）（a＞0且a≠1）的定义域为（$\frac{3}{2}$，+∞），图象过的定点为（2，0）．分析 根据对数函数的性质求出函数的定义域即可，根据2x-3=1，求出函数恒过定点（2，0）．
解答 解：由题意得：2x-3＞0，解得：x＞$\frac{3}{2}$，
故函数的定义域是：$（\frac{3}{2}，+∞）$；
令2x-3=1，解得：x=2，此时，f（2）=0，
故函数图象恒过（2，0），
故答案为：（$\frac{3}{2}$，+∞），（2，0）．
点评 本题考查了求导数函数的定义域问题，考查对数函数的性质，是一道基础题．
练习册系列答案
相关题目
19．
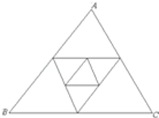如图，已知△ABC周长为2，连接△ABC三边的中点构成第二个三角形，再连接第二个对角线三边中点构成第三个三角形，依此类推，第2003个三角形周长为（ ）
如图，已知△ABC周长为2，连接△ABC三边的中点构成第二个三角形，再连接第二个对角线三边中点构成第三个三角形，依此类推，第2003个三角形周长为（ ）| A． | $\frac{1}{2002}$ | B． | $\frac{1}{2001}$ | C． | $\frac{1}{{2}^{2002}}$ | D． | 2${\;}^{\frac{1}{2001}}$ |
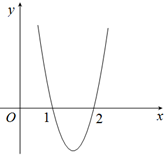已知函数f（x）=2x3+bx2+cx，其导函数y=f′（x）的图象（如图所示）经过点（1，0），（2，0）．
原始社会时期，人们通过在绳子上打结来计算数量，即“结绳计数”，当时有位父亲，为了准确记录孩子的成长天数，在粗细不同的绳子上打结，由细到粗，满七进一，如图所示，孩子已经出生468天．