题目内容

7．如图，在平行四边形ABCD中，点E在AB上且EB=2AE，AC与DE交于点F，则△CDF的周长与△AEF的周长之比为（　　）
A．1：3B．3：1C．1：2D．2：1

分析 证明△CDF∽△AEF，可求△CDF的周长与△AEF的周长之比．

解答 解：∵四边形ABCD是平行四边形，EB=2AE，
∴AB∥CD，CD=3AE，
∴△CDF∽△AEF，
∴△CDF的周长与△AEF的周长之比=CD：AE=3：1．
故选B．

点评 本题考查三角形相似的判断，考查学生的计算能力，属于基础题．

练习册系列答案
相关题目
17．已知椭圆4x2+y2=1及直线y=x+m．
（1）直线和椭圆有公共点，求实数m的取值范围；
（2）若m=$\frac{\sqrt{2}}{2}$，求直线被椭圆截得的弦长．
18．若不等式|x+2|-|x-1|≥a3-4a2-3对任意实数x恒成立，则实数a的取值范围是（　　）
A．（-∞，4]B．（-∞，2]C．[4，+∞）D．[2，+∞）
15．已知函数f（x）=$\frac{1}{2}$ax2+lnx，其中a∈R．
（1）求函数f（x）的单调区间；
（2）若a＜-1，f（x）在（0，1]上的最大值为-1，求a的值．
2．已知函数f（x）=$\frac{lnx}{x}$．
（1）当e≤x≤e2时，求函数f（x）的最小值；
（2）已知函数g（x）=2x-$\frac{ax（x-1）}{lnx}$，且f（x）g（x）≤0恒成立，求实数a的值；
（3）某同学发现：存在正实数m、n（m＜n），使mn=nm，试问：他的发现是否正确？若不正确，则请说明理由；若正确，则请直接写出m的取值范围，而不需要解答过程．
12．已知f（x）=$\frac{2}{3}$x3-2ax2-3x（a∈R）．
（Ⅰ）若f（x）在区间（-1，1）内为减函数，求实数a的取值范围；
（Ⅱ）对于实数a的不同取值，试讨论y=f（x）在（-1，1）内的极值点的个数．
19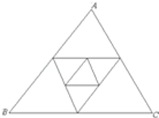．如图，已知△ABC周长为2，连接△ABC三边的中点构成第二个三角形，再连接第二个对角线三边中点构成第三个三角形，依此类推，第2003个三角形周长为（　　）
A．$\frac{1}{2002}$B．$\frac{1}{2001}$C．$\frac{1}{{2}^{2002}}$D．2${\;}^{\frac{1}{2001}}$
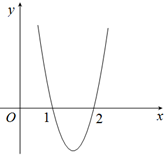16．已知函数f（x）=2x3+bx2+cx，其导函数y=f′（x）的图象（如图所示）经过点（1，0），（2，0）．
（Ⅰ）求f（x）的解析式；
（Ⅱ）若方程f（x）-m=0恰有2个根，求m的值．
17．已知函数f（x）=x+$\frac{1}{x-a}$+$\frac{1}{x-b}$（a，b为实常数）．
（Ⅰ）若a+b=0，判断函数f（x）的奇偶性，并加以证明；
（Ⅱ）记M=$\left\{\begin{array}{l}{a，b＜a}\\{b，b≥a}\end{array}\right.$，A=$\frac{a+b}{2}$，求实数λ的取值范围，使得方程f（x）=$\frac{λ}{x-A}$+A在区间（M，+∞）上无解．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网