题目内容
10. 如图,△ABC是边长为2的等边三角形,△ABD是等腰直角三角形,AD⊥BD,平面ABC⊥平面ABD,且EC⊥平面ABC,EC=1.
如图,△ABC是边长为2的等边三角形,△ABD是等腰直角三角形,AD⊥BD,平面ABC⊥平面ABD,且EC⊥平面ABC,EC=1.(Ⅰ)证明:DE∥平面ABC;
(Ⅱ)证明:平面ABD⊥平面BDE.
分析 (I)取AB的中点F,连结DF,CF,利用面面垂直的性质得出DF⊥平面ABC,故而DF∥EC,通过计算DF的值可得DF=EC,于是四边形DFCE为平行四边形,得出DE∥CF,得出结论.
(II)利用面面垂直的性质得出CF⊥平面ABD,而CF∥DE.故而DE⊥平面ABD,于是结论得证.
解答 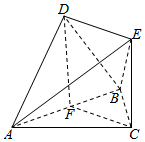 证明:(I)取AB的中点F,连结DF,CF,
证明:(I)取AB的中点F,连结DF,CF,
∵AD=BD,F是AB的中点,
∴DF⊥AB,
又∵平面ABC⊥平面ABD,平面ABC∩平面ABD=AB,DF?平面ABD,
∴DF⊥平面ABC,又∵EC⊥平面ABC,
∴DF∥EC.
∵△ABD是等腰直角三角形,AB=2,
∴DF=$\frac{1}{2}$AB=1,又EC=1,
∴DF=EC,
∴四边形DFCE是平行四边形,
∴DE∥CF,又DE?平面ABC,CF?平面ABC,
∴DE∥平面ABC.
(II)∵△ABC是等边三角形,F是AB的中点,
∴CF⊥AB,
又平面ABC⊥平面ABD,平面ABC∩平面ABD=AB,CF?平面ABC,
∴CF⊥平面ABD,又CF∥ED,
∴DE⊥平面ABD,又DE?平面BDE,
∴平面ABD⊥平面BDE.
点评 本题考查了线面平行,面面垂直的判定,构造平行线与垂线是证明的关键.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
5.在菱形ABCD中,A=60°,AB=2$\sqrt{3}$,将△ABD沿BD折起到△PBD的位置,若二面角P-BD-C的大小为120°,则三棱锥P-BCD的外接球体积为( )
| A. | $\frac{28\sqrt{7}}{3}$π | B. | 28$\sqrt{7}$π | C. | $\frac{32}{3}$π | D. | 4$\sqrt{3}$π |
15.下列函数中,既是奇函数又在R上单调递减的是( )
| A. | y=$\frac{1}{x}$ | B. | y=e-x | C. | y=-x3 | D. | y=lnx |
2.若2sin2α=1-cos2α,则tanα等于( )
| A. | -2 | B. | 2 | C. | -2或0 | D. | 2或0 |
 中国传统文化中很多内容体现了数学的对称美,如图所示的太极图是由黑白两个鱼形纹组成的圆形图案,充分展现了相互转化、对称统一的形式美、和谐美.给出定义:能够将圆O的周长和面积同时平分的函数称为这个圆的“优美函数”.给出下列命题:
中国传统文化中很多内容体现了数学的对称美,如图所示的太极图是由黑白两个鱼形纹组成的圆形图案,充分展现了相互转化、对称统一的形式美、和谐美.给出定义:能够将圆O的周长和面积同时平分的函数称为这个圆的“优美函数”.给出下列命题: